题目内容
已知⊙O的半径是1，△ABC内接于圆O．若∠B=34°，∠C=110°，则弧BC的长为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
考点：弧长的计算,圆周角定理
专题：
分析：先求出∠A的度数，然后根据圆周角定理求出∠BOC的度数，继而运用弧长公式求出弧BC的长度．
解答：解：
由题意得，∠A=180°-∠B-∠C=180°-34°-110°=36°，
则∠BOC=2∠A=72°，
则弧BC的长=
=
π．
故选B．
由题意得，∠A=180°-∠B-∠C=180°-34°-110°=36°，则∠BOC=2∠A=72°，
则弧BC的长=
| 72π×1 |
| 180 |
| 2 |
| 5 |
故选B．
点评：本题考查了弧长的计算以及圆周角定理，解答本题的关键是掌握弧长公式．
练习册系列答案
相关题目
如图，AB⊥CD于O，EF为过点O的直线，MN平分∠AOC，若∠EON=100°，那么∠EOB=
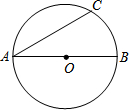如图，AB是圆O的直径，AC是圆O的弦，AB=2，∠BAC=30°．在图中画出弦AD，使AD=1，则∠CAD的度数为（ ）| A、30° |
| B、60° |
| C、60°或90° |
| D、30°或90° |
如图，大正方形的边长为m，小正方形的边长为n，若用x、y表示四个长方形的两边长（x＞y），观察图案及以下关系式：①x-y=n；②xy=| m2-n2 |
| 4 |
| m2-n2 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
在直角坐标系中，O为坐标原点A（1，3），在x轴上确定一点P，使△AOP为等腰三角形，则符合条件的点P共有（ ）
| A、4个 | B、3个 | C、2个 | D、5个 |
已知：x2+4x+y2-8y+20=0，则
=（ ）
| x |
| y |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|