题目内容
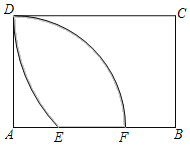
【题目】在矩形
中，
，
，点
是边
上一点，
交
于点
，点
在射线
上，且
是
和
的比例中项．
（1）如图1，求证：
；
（2）如图2，当点在线段之间，联结
，且与
互相垂直，求
的长；
（3）联结，如果
与以点、、为顶点所组成的三角形相似，求
的长．
【答案】（1）详见解析；（2）
；（3）
的长分别为
或3．
【解析】
（1）由比例中项知
，据此可证
得
，再证明
可得答案；
（2）先证
，结合
，得
，从而知
，据此可得
，由（1）得，据此知 ，求得 ；
（3）分
和
两种情况分别求解可得．
（1）证明：∵
是
和
的比例中项
∴
∵
∴
∴
∵
∴
∵
∴
∴
∴
（2）解：∵
与
互相垂直
∴
∵
∴
∴
由（1）得
∴
∴
∴
∵
，
，
∴
∴
由（1）得
∴
∴
∴
∵
∴
∴
（3）∵
，
又
，由（1）得
∴
当
与以点
、
、
为顶点所组成的三角形相似时
1) ，如图
∴
由（2）得：
2），如图
过点作
，垂足为点
由（1）得
∴
∴
又
设
，则
，
，
又
∴
，解得
∴
综上所述，的长分别为或3．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
