Question

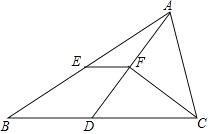
【题目】《九章算术》是中国传统数学最重要的著作，在“勾股”章中有这样一个问题：“今有邑方二百步，各中开门，出东门十五步有木，问：出南门几步而见木？”

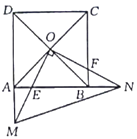
用今天的话说，大意是：如图，是一座边长为200步（“步”是古代的长度单位）的正方形小城，东门位于的中点，南门位于的中点，出东门15步的处有一树木，求出南门多少步恰好看到位于处的树木（即点在直线上）？请你计算的长为__________步．

Answer 1

【答案】

【解析】由正方形的性质得到∠EDG=90°，从而∠KDC+∠HDA=90°，再由∠C+∠KDC=90°，得到∠C=∠HDA，即有△CKD∽△DHA，由相似三角形的性质得到CK：KD=HD：HA，求解即可得到结论．

∵DEFG是正方形，∴∠EDG=90°，∴∠KDC+∠HDA=90°．

∵∠C+∠KDC=90°，∴∠C=∠HDA．

∵∠CKD=∠DHA=90°，∴△CKD∽△DHA，

∴CK：KD=HD：HA，∴CK：100=100：15，

解得：CK=．

故答案为：．