题目内容
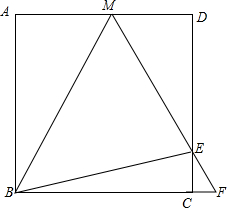 如图,正方形ABCD边长为12,点M为AD上一点,E为CD上一点,∠MBE=45°,ME、BC的延长线相交于点F,若ME=10,则S△MDE与S△CEF的面积之和为多少?
如图,正方形ABCD边长为12,点M为AD上一点,E为CD上一点,∠MBE=45°,ME、BC的延长线相交于点F,若ME=10,则S△MDE与S△CEF的面积之和为多少?考点:四边形综合题
专题:综合题
分析:先根据正方形的性质得BA=BC,∠ABC=90°,则可将△BCE逆时针旋转90°得到△BAN,如图,根据旋转的性质得BN=BE,EC=AN,∠NBE=90°,∠BAN=∠BCE=90°,所以点N在DA的延长线上,即有MN=AM+AN,再利用”SAS“证明△BMN≌△BME,得到MN=ME=10,则AM+CE=10,设EC=x,可得到AM=10-x,DM=2+x,DE=12-x,在Rt△MDE中利用勾股定理得(2+x)2+(12-x)2=100,整理得x2-10x+24=0,解得:x1=4,x2=6,即当CE=4时,DE=8,DM=6;当CE=6时,DE=6,DM=8,然后证明△MDE∽△FCE,利用相似比可计算出CF=3或CF=8,即当CE=4时,DE=8,DM=6,CF=3,当CE=6时,DE=6,DM=8,CF=8,最后根据三角形面积公式进行计算.
解答: 解:∵四边形ABCD为正方形,
解:∵四边形ABCD为正方形,
∴BA=BC,∠ABC=90°,
∴将△BCE逆时针旋转90°得到△BAN,如图,
∴BN=BE,EC=AN,∠NBE=90°,∠BAN=∠BCE=90°,
∴点N在DA的延长线上,
∴MN=AM+AN,
∵∠MBE=45°,
∴∠NBM=90°-45°=45°,
在△BMN和△BME中,
,
∴△BMN≌△BME,
∴MN=ME=10,
而MN=AN+AM=CE+AM,
∴AM+CE=10,
设EC=x,则AM=10-x,DM=AD-AM=12-(10-x)=2+x,DE=CD-EC=12-x,
在Rt△MDE中,∵ME2=DM2+DE2,
∴(2+x)2+(12-x)2=100,
整理得x2-10x+24=0,解得:x1=4,x2=6,
当CE=4时,DE=8,DM=6;
当CE=6时,DE=6,DM=8,
∵AD∥BC,
∴△MDE∽△FCE,
∴
=
,即
=
或
=
,
∴CF=3或CF=8,
当CE=4时,DE=8,DM=6,CF=3,此时S△MDE与S△CEF的面积之和=
×8×6+
×3×4=30;
当CE=6时,DE=6,DM=8,CF=8,此时S△MDE与S△CEF的面积之和=
×6×8+
×8×6=48,
∴S△ADE+S△CEF=30或48.
 解:∵四边形ABCD为正方形,
解:∵四边形ABCD为正方形,∴BA=BC,∠ABC=90°,
∴将△BCE逆时针旋转90°得到△BAN,如图,
∴BN=BE,EC=AN,∠NBE=90°,∠BAN=∠BCE=90°,
∴点N在DA的延长线上,
∴MN=AM+AN,
∵∠MBE=45°,
∴∠NBM=90°-45°=45°,
在△BMN和△BME中,
|
∴△BMN≌△BME,
∴MN=ME=10,
而MN=AN+AM=CE+AM,
∴AM+CE=10,
设EC=x,则AM=10-x,DM=AD-AM=12-(10-x)=2+x,DE=CD-EC=12-x,
在Rt△MDE中,∵ME2=DM2+DE2,
∴(2+x)2+(12-x)2=100,
整理得x2-10x+24=0,解得:x1=4,x2=6,
当CE=4时,DE=8,DM=6;
当CE=6时,DE=6,DM=8,
∵AD∥BC,
∴△MDE∽△FCE,
∴
| MD |
| CF |
| DE |
| CE |
| 6 |
| CF |
| 8 |
| 4 |
| 8 |
| CF |
| 6 |
| 6 |
∴CF=3或CF=8,
当CE=4时,DE=8,DM=6,CF=3,此时S△MDE与S△CEF的面积之和=
| 1 |
| 2 |
| 1 |
| 2 |
当CE=6时,DE=6,DM=8,CF=8,此时S△MDE与S△CEF的面积之和=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ADE+S△CEF=30或48.
点评:本题考查了四边形的综合题:熟练掌握正方形的性质、旋转的性质和三角形全等的判定与性质;会运用勾股定理和相似比进行计算.

练习册系列答案
相关题目
 如图,AD是△ABC的角平分线,E是BC边上一动点,过点E作直线EF∥AD,分别交射线CA和BA于点F和G,CH∥AB,交直线EF于点H.
如图,AD是△ABC的角平分线,E是BC边上一动点,过点E作直线EF∥AD,分别交射线CA和BA于点F和G,CH∥AB,交直线EF于点H. 如图,x轴是西气东输工程天然气的主管道,按规定主管道在我市只允许开一个口,A(2,1),B(10,5)是我市新建的两个天然气站,现在要在x轴上选一个点开口,分别连接到A、B,小明说:“作AB的垂直平分线交x轴于C,就选点C,C点到A、B的距离相等.“小华说:“不行,可以用轴对称知识做出点E,点E到A、B的距离之和最小,这样可以节约原材料,节省费用.“请你求出:
如图,x轴是西气东输工程天然气的主管道,按规定主管道在我市只允许开一个口,A(2,1),B(10,5)是我市新建的两个天然气站,现在要在x轴上选一个点开口,分别连接到A、B,小明说:“作AB的垂直平分线交x轴于C,就选点C,C点到A、B的距离相等.“小华说:“不行,可以用轴对称知识做出点E,点E到A、B的距离之和最小,这样可以节约原材料,节省费用.“请你求出: