题目内容
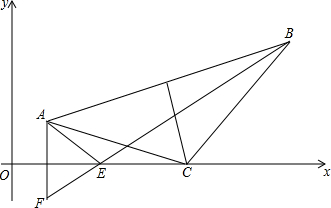 如图,x轴是西气东输工程天然气的主管道,按规定主管道在我市只允许开一个口,A(2,1),B(10,5)是我市新建的两个天然气站,现在要在x轴上选一个点开口,分别连接到A、B,小明说:“作AB的垂直平分线交x轴于C,就选点C,C点到A、B的距离相等.“小华说:“不行,可以用轴对称知识做出点E,点E到A、B的距离之和最小,这样可以节约原材料,节省费用.“请你求出:
如图,x轴是西气东输工程天然气的主管道,按规定主管道在我市只允许开一个口,A(2,1),B(10,5)是我市新建的两个天然气站,现在要在x轴上选一个点开口,分别连接到A、B,小明说:“作AB的垂直平分线交x轴于C,就选点C,C点到A、B的距离相等.“小华说:“不行,可以用轴对称知识做出点E,点E到A、B的距离之和最小,这样可以节约原材料,节省费用.“请你求出:(1)C点的坐标;
(2)AE+BE的值.
考点:相似形综合题
专题:
分析:(1)作BG⊥x轴,设C(x,0),则HC=x-2,GC=10-x,在Rt△AHC和Rt△BGC中,运用勾股定理即可求出x的值.
(2)根据△HEF∽△GEB,再利用勾股定理求出AE和BE的值.
(2)根据△HEF∽△GEB,再利用勾股定理求出AE和BE的值.
解答: 解:(1)如图,作BG⊥x轴,设C(x,0),则HC=x-2,GC=10-x,
解:(1)如图,作BG⊥x轴,设C(x,0),则HC=x-2,GC=10-x,
∵AC=CB,
∴在Rt△AHC和Rt△BGC中,
12+(x-2)2=(10-x)2+52,
即x=7.5,可得C点坐标为(7.5,0).
(2)∵△HEF∽△GEB,
∴
=
=
,
又HE+EG=HG=10-2=8,
∴
EG+EG=8,EG=
,HE=
,AE=
=
;BE=
=
,
从而AE+BE=
+
=10.
 解:(1)如图,作BG⊥x轴,设C(x,0),则HC=x-2,GC=10-x,
解:(1)如图,作BG⊥x轴,设C(x,0),则HC=x-2,GC=10-x,∵AC=CB,
∴在Rt△AHC和Rt△BGC中,
12+(x-2)2=(10-x)2+52,
即x=7.5,可得C点坐标为(7.5,0).
(2)∵△HEF∽△GEB,
∴
| HE |
| EG |
| HF |
| GB |
| 1 |
| 5 |
又HE+EG=HG=10-2=8,
∴
| 1 |
| 5 |
| 20 |
| 3 |
| 4 |
| 3 |
12+(
|
| 5 |
| 3 |
52+(
|
| 25 |
| 3 |
从而AE+BE=
| 5 |
| 3 |
| 25 |
| 3 |
点评:本题考查了相似形,找到相关的三角形,作出恰当的辅助线,灵活运用勾股定理是解题的关键.

练习册系列答案
相关题目
大于-4且小于5的整数一共有( )
| A、6个 | B、7个 | C、8个 | D、9个 |
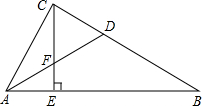 如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,CE⊥AB,垂足为E,交AD于点F,试猜想△CFD的形状,证明你的结论.
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,CE⊥AB,垂足为E,交AD于点F,试猜想△CFD的形状,证明你的结论.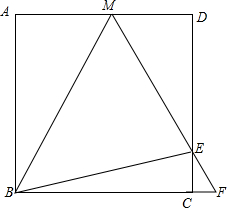 如图,正方形ABCD边长为12,点M为AD上一点,E为CD上一点,∠MBE=45°,ME、BC的延长线相交于点F,若ME=10,则S△MDE与S△CEF的面积之和为多少?
如图,正方形ABCD边长为12,点M为AD上一点,E为CD上一点,∠MBE=45°,ME、BC的延长线相交于点F,若ME=10,则S△MDE与S△CEF的面积之和为多少? 如图,有三种卡片,其中边长为a的正方形卡片1张,长、宽分别为a、b的正方形4张,边长为b的正方形卡片4张,若用这9张卡片拼成一个正方形,求该正方形的面积.
如图,有三种卡片,其中边长为a的正方形卡片1张,长、宽分别为a、b的正方形4张,边长为b的正方形卡片4张,若用这9张卡片拼成一个正方形,求该正方形的面积.