题目内容
如图，在平行四边形ABCD中，E在DC上，若DE：EC=2：3，则S△CEF：S△ABF=考点：相似三角形的判定与性质,平行四边形的性质
专题：
分析：利用平行四边形的性质得出AB=CD，AB∥CD，即可得出△CEF∽△ABF，进而利用相似三角形的性质求出即可．
解答：解：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
∴△CEF∽△ABF，
∵DE：EC=2：3，
∴
=
，
∴S△CEF：S△ABF=9：25．
故答案为：9：25．
∴AB=CD，AB∥CD，
∴△CEF∽△ABF，
∵DE：EC=2：3，
∴
| CE |
| AB |
| 3 |
| 5 |
∴S△CEF：S△ABF=9：25．
故答案为：9：25．
点评：此题主要考查了平行四边形的性质以及相似三角形的判定与性质，得出△CEF∽△ABF是解题关键．
练习册系列答案
相关题目
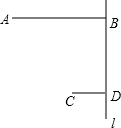如图，A村到公路l的距离AB为6km，C村到公路l的距离CD为2km，且BD的长为6km．现要在公路l上取一点P，使AP+CP的值最小，则这个最小值为
如图，正方形ABCD是一块绿化带，其中阴影部分EOFB，GHMN都是正方形的花圃．已知自由飞翔的小鸟，将随机落在这块绿化带上，则小鸟在花圃上的概率为
如图，圆柱的高为10cm，底面半径为2cm．在下底面的A点处有一只蚂蚁，它想吃到上底面上与A点相对的B点处，需要爬行的最短路程是下列从左边到右边的变形属于因式分解的是（ ）
| A、（m+2）（m-2）=m2-4 |
| B、am+bm+cm=m（a+b+c） |
| C、m2-4m+4=m（m-4）+4 |
| D、a2+b2=（a+b）2-2ab |