题目内容
如图，正方形ABCD是一块绿化带，其中阴影部分EOFB，GHMN都是正方形的花圃．已知自由飞翔的小鸟，将随机落在这块绿化带上，则小鸟在花圃上的概率为考点：几何概率
专题：
分析：求得阴影部分的面积与正方形ABCD的面积的比即可求得小鸟在花圃上的概率．
解答：解：设正方形的ABCD的边长为a，
则BF=
BC=
，AN=NM=MC=
a，
∴阴影部分的面积为（
）2+（
a）2=
a2，
∴小鸟在花圃上的概率为
=
，
故答案为：
．
则BF=
| 1 |
| 2 |
| a |
| 2 |
| ||
| 3 |
∴阴影部分的面积为（
| a |
| 2 |
| ||
| 3 |
| 17 |
| 36 |
∴小鸟在花圃上的概率为
| ||
| a2 |
| 17 |
| 36 |
故答案为：
| 17 |
| 36 |
点评：本题考查了正方形的性质及几何概率，关键是表示出大正方形的边长，从而表示出两个阴影正方形的边长，最后表示出面积．
练习册系列答案
相关题目
如图，在数轴上1，
如图，在平行四边形ABCD中，E在DC上，若DE：EC=2：3，则S△CEF：S△ABF=
如图，直线a、b、c、d，已知c⊥a，c⊥b，直线b、c、d交于一点，若∠1=60°，则∠2等于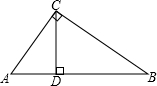
如图，在Rt△ABC中，∠C=90°，AC=6、BC=8，CD⊥AB，则CD=已知tan（α-15°）=1，则锐角α的度数为（ ）
| A、30° | B、60° |
| C、45° | D、75° |