题目内容
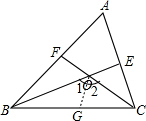
 △ABC中,∠A=60°,平分线BE、CF相交于O,求证:OE=OF.
△ABC中,∠A=60°,平分线BE、CF相交于O,求证:OE=OF.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:由∠A=60°,BE、CF是角平分线就可以得出∠BOC=120,进而得出∠BOF=∠COE=60°,在BC上取点G,使BG=BF,就可以得出△BOF≌△BOG,就可以得出OF=OG,∠BOF=∠1=60°,进而求出∠2=60°,得出∠2=∠COE,得出△COE≌△COG,就有OE=OG,进而得出结论.
解答:证明:在BC上取点G,使BG=BF.
∵BE平分∠ABC,CF∠ACB,
∴∠ABE=∠CBE=
∠ABC,∠ACF=∠BCF=
∠ACB.
∵∠A=60°,
∴∠ABC+∠ACB=120°,
∴
∠ABC+
∠ACB=60°,
∴∠BOC=120°.
∴∠BOF=∠COE=60°.
在△BOF和△BOG中
,
∴△BOF≌△BOG(SAS),
∴OF=OG,∠BOF=∠1,
∴∠1=60°,
∴∠2=60°,
∴∠2=∠COE,
在△COE和△COG中
,
∴△COE≌△COG(ASA),
∴OE=OG.
∴OE=EF.
∵BE平分∠ABC,CF∠ACB,
∴∠ABE=∠CBE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠A=60°,
∴∠ABC+∠ACB=120°,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=120°.
∴∠BOF=∠COE=60°.
在△BOF和△BOG中
|

∴△BOF≌△BOG(SAS),
∴OF=OG,∠BOF=∠1,
∴∠1=60°,
∴∠2=60°,
∴∠2=∠COE,
在△COE和△COG中
|
∴△COE≌△COG(ASA),
∴OE=OG.
∴OE=EF.
点评:本题考查了角平分线的性质的运用,邻补角的性质的运用,三角形的内角和定理的运用,全等三角形的判定与性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
已知抛物线y=a(x-2)2+6经过点(3,3).
(1)求a的值;
(2)求方程a(x-2)2+6=0的解;
(3)若点A(m,y1),B(n,y2)都在该抛物线上,且2<n<m,试比较y1与y2的大小.
(1)求a的值;
(2)求方程a(x-2)2+6=0的解;
(3)若点A(m,y1),B(n,y2)都在该抛物线上,且2<n<m,试比较y1与y2的大小.
 如图,已知∠1=∠2=90°,∠3=123°,则∠4等于( )
如图,已知∠1=∠2=90°,∠3=123°,则∠4等于( )| A、33° | B、57° |
| C、123° | D、147° |
如果一个n边形每个外角都是30°,那么n的值是( )
| A、11 | B、12 | C、13 | D、14 |
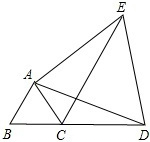 如图所示,△ABC为等边三角形,D是BC延长线上一点,连接AD,以AD为边作等边△ADE.连接CE.求证:CE=AC+CD.
如图所示,△ABC为等边三角形,D是BC延长线上一点,连接AD,以AD为边作等边△ADE.连接CE.求证:CE=AC+CD.

 如图,图中有哪些同位角,内错角,同旁内角?并写出(至少各写出四对)
如图,图中有哪些同位角,内错角,同旁内角?并写出(至少各写出四对)