题目内容
阅读材料,在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1-x2|是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离,如图,过A,B分别向x轴、y轴作垂线AM1、AN1和
BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1-x2|,BQ=|y1-y2|,
∴AB2=AQ2+BQ2=|x1-x2|+|y1-y2|2=(x1-x2|2+(y1-y2)2,
由此得到平面直角坐标系内任意两点A(x1,y1),B(x2,y2)间的距离公式为:AB= .
(1)直接应用平面内两点间距离公式计算点A(1,-3),B(-2,1)之间的距离为 ;
(2)利用上面公式,在平面直角坐标系中的两点A(0,3),B(4,1),P为x轴上任一点,则PA+PB的最小值和此时P点的坐标;
(3)应用平面内两点间的距离公式,求代数式
+
的最小值.

BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1-x2|,BQ=|y1-y2|,
∴AB2=AQ2+BQ2=|x1-x2|+|y1-y2|2=(x1-x2|2+(y1-y2)2,
由此得到平面直角坐标系内任意两点A(x1,y1),B(x2,y2)间的距离公式为:AB=
(1)直接应用平面内两点间距离公式计算点A(1,-3),B(-2,1)之间的距离为
(2)利用上面公式,在平面直角坐标系中的两点A(0,3),B(4,1),P为x轴上任一点,则PA+PB的最小值和此时P点的坐标;
(3)应用平面内两点间的距离公式,求代数式
| x2+(y-2)2 |
| (x-3)2+(y-1)2 |

考点:轴对称-最短路线问题,两点间的距离
专题:
分析:(1)直接利用两点之间距离公式直接求出即可;
(2)利用轴对称求最短路线方法得出P点位置,进而求出PA+PB的最小值;
(3)根据原式表示的几何意义是点(x,y)到点(-2,-4)和(3,1)的距离之和,当点(x,y)在以(-2,-4)和(3,1)为端点的线段上时其距离之和最小,进而求出即可.
(2)利用轴对称求最短路线方法得出P点位置,进而求出PA+PB的最小值;
(3)根据原式表示的几何意义是点(x,y)到点(-2,-4)和(3,1)的距离之和,当点(x,y)在以(-2,-4)和(3,1)为端点的线段上时其距离之和最小,进而求出即可.
解答:解:(1))∵平面直角坐标系内任意两点A(x1,y1),B(x2,y2)间的距离公式为:
∴点A(1,-3),B(-2,1)之间的距离为:AB=5;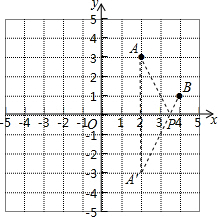
故答案为:5;
(2)如图,作点B关于x轴对称的点B,连接AB,直线AB,于x轴的交点即为所求的点P.
∵B(4,1)∴B,(4,-1),
∵A(0,3)∴设直线AB,的一次函数表达式为y=kx+3,
把B,(4,-1)代入-1=4k+3 解得 k=-1,
当y=0时,解得x=3,即P(3,0),
∴PA+PB=PA+PB,=AB,=
=4
,
即为PA+PB的最小值为4
.
故答案为:4
;
(3)原式=
+
,
故原式表示点(x,y)到(0,2)和(3,1)的距离之和.由两点之间线段最短,点(x,y)在以(0,2)和(3,1)为端点的线段上时,原式值最小.利用公式,原式=
.
∴点A(1,-3),B(-2,1)之间的距离为:AB=5;

故答案为:5;
(2)如图,作点B关于x轴对称的点B,连接AB,直线AB,于x轴的交点即为所求的点P.
∵B(4,1)∴B,(4,-1),
∵A(0,3)∴设直线AB,的一次函数表达式为y=kx+3,
把B,(4,-1)代入-1=4k+3 解得 k=-1,
当y=0时,解得x=3,即P(3,0),
∴PA+PB=PA+PB,=AB,=
| (0-4)2+(3+1)2 |
| 2 |
即为PA+PB的最小值为4
| 2 |
故答案为:4
| 2 |
(3)原式=
| (x-0)2+(y-2)2 |
| (x-3)2+(y-1)2 |
故原式表示点(x,y)到(0,2)和(3,1)的距离之和.由两点之间线段最短,点(x,y)在以(0,2)和(3,1)为端点的线段上时,原式值最小.利用公式,原式=
| 10 |
点评:此题主要考查了利用轴对称求最值问题以及两点之间距离公式,正确转化代数式为两点之间距离问题是解题关键.

练习册系列答案
相关题目
下列计算正确的是( )
| A、a2•(-a)2=a4 |
| B、-a8+a4=-a4 |
| C、(2a2)3=6a6 |
| D、a2•a3=a6 |
下列算式正确的是( )
| A、0-(-3)=-3 | ||||||
| B、5+(-5)=0 | ||||||
C、-
| ||||||
| D、-5-(-3)=-8 |
 如图,等边△ABC中,AB=4,D是BC的中点,将△ABD绕点A逆时针旋转60°得△ACE,那么线段DE的长为
如图,等边△ABC中,AB=4,D是BC的中点,将△ABD绕点A逆时针旋转60°得△ACE,那么线段DE的长为 如图,在平行四边形ABCD中,E为AD的中点,BD=15,则BF=
如图,在平行四边形ABCD中,E为AD的中点,BD=15,则BF=