题目内容
18．
菱形OACB在平面直角坐标系中的位置如图所示，点C的坐标是（4，0），点A的纵坐标是1，则点B的坐标是（ ）| A． | （2，1） | B． | （2，-1） | C． | （1，-2） | D． | （1，2） |
分析 根据菱形的性质求出OD=$\frac{1}{2}$OC=2，OB=OA=1，即可得出点B的坐标．
解答 解：连接AB交OC于D，如图所示：
点C的坐标是（4，0），点A的纵坐标是1，
∴OC=4，OA=1，
∵四边形OACB是菱形，
∴OC⊥AB，OD=$\frac{1}{2}$OC=2，OB=OA=1，
∴点B的坐标是（2，-1）；
故选：B．
点评 本题考查了菱形的性质、坐标与图形性质；熟练掌握菱形的性质是解决问题的关键．
练习册系列答案
相关题目
9．设A（-3，y1），B（0，y2），C（1，y3）是抛物线y=-（x+1）2+m上的三点，则y1，y2，y3的大小关系为（ ）
| A． | y1=y2＞y3 | B． | y1=y3＜y2 | C． | y1=y3=y2 | D． | y1＞y2＞y3 |
6．已知m-2n=-1，则代数式1-2m+4n的值是（ ）
| A． | -3 | B． | -1 | C． | 2 | D． | 3 |
3．
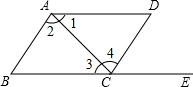如图，点E在BC的延长线上，下列条件中能判断AB∥CD的是（ ）
如图，点E在BC的延长线上，下列条件中能判断AB∥CD的是（ ）| A． | ∠1=∠3 | B． | ∠D=∠DCE | C． | ∠2=∠4 | D． | ∠D+∠BCD=180° |
如图，△ABC是以BC为底边的等腰三角形，点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点，点B在二次函数y=$\frac{1}{8}$x2+bx+c的图象上，且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形．