题目内容
13.先化简,再求值:$\frac{{x}^{2}-4x+4}{{x}^{2}-4}$÷$\frac{x-2}{{x}^{2}+2x}$+3,在0、±1、±2五个数中选择一个恰当的数x代入求值.(所选的x要使分式有意义)分析 先对分子分母因式分解,再约分,根据分母不为0,选择x的值代入计算即可.
解答 解:原式=$\frac{(x-2)^{2}}{(x+2)(x-2)}$•$\frac{x(x+2)}{x-2}$+3
=x+3,
∵x≠±2,0,
∴x=1,
∴原式=x+3=1+3=4.
点评 本题考查了分式的化简求值,因式分解和约分是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列等式中y是x的反比例函数的是( )
| A. | y=4x | B. | $\frac{y}{x}$=3 | C. | y=6x+1 | D. | xy=2 |
18. 菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(4,0),点A的纵坐标是1,则点B的坐标是( )
菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(4,0),点A的纵坐标是1,则点B的坐标是( )
 菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(4,0),点A的纵坐标是1,则点B的坐标是( )
菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(4,0),点A的纵坐标是1,则点B的坐标是( )| A. | (2,1) | B. | (2,-1) | C. | (1,-2) | D. | (1,2) |
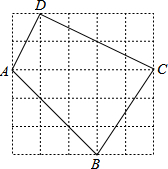 如图,每个小方格都是边长为1的正方形.
如图,每个小方格都是边长为1的正方形.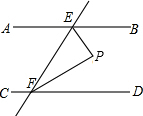 已知:如图,直线EF分别交AB,CD于点E,F,且∠AEF=66°,∠BEF的平分线与∠DFE的平分线相交于点P.
已知:如图,直线EF分别交AB,CD于点E,F,且∠AEF=66°,∠BEF的平分线与∠DFE的平分线相交于点P.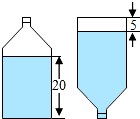 有种饮料瓶如图,它的直径是4cm,里面的水高度是20cm,把瓶盖拧紧倒置放平,无水部分圆柱高度是5cm,求饮料瓶的容积是多少?(结果保留整数)
有种饮料瓶如图,它的直径是4cm,里面的水高度是20cm,把瓶盖拧紧倒置放平,无水部分圆柱高度是5cm,求饮料瓶的容积是多少?(结果保留整数)