题目内容
14. 如图,△ABC是等边三角形,BD⊥AC于点D,E为BC的中点,连接DE.求证:DE=DC.
如图,△ABC是等边三角形,BD⊥AC于点D,E为BC的中点,连接DE.求证:DE=DC.
分析 根据等边三角形的性质得到AC=BC,CD=$\frac{1}{2}$AC,∠BDC=90°,根据直角三角形的性质得到DE=$\frac{1}{2}$BC,于是得到结论.
解答 解:∵△ABC是等边三角形,
∴AC=BC,
∵BD⊥AC于点D,
∴CD=$\frac{1}{2}$AC,∠BDC=90°,
∵E为BC的中点,
∴DE=$\frac{1}{2}$BC,
∴DE=DC.
点评 本题考查了等边三角形的性质,直角三角形的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
9.两个锐角分别相等的两个直角三角形( )全等.
| A. | 不一定 | B. | 一定不 | C. | 一定 | D. | 以上都不对 |
3. 已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为( )
已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为( )
 已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为( )
已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为( )| A. | 3 | B. | 5 | C. | 6 | D. | 10 |
 已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为5.
已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为5. 已知:如图,BC∥EF,AD=BE,BC=EF,试证明AC=DF.
已知:如图,BC∥EF,AD=BE,BC=EF,试证明AC=DF.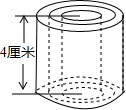 如图所示,圆柱的高是4厘米,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化.
如图所示,圆柱的高是4厘米,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化.