题目内容
5.如果把四个不等于0的数m、n、x、y组成的等积式mx=ny写成比例式,那么正确的是( )| A. | $\frac{x}{y}$=$\frac{n}{m}$ | B. | $\frac{x}{y}$=$\frac{m}{n}$ | C. | $\frac{x}{m}$=$\frac{y}{n}$ | D. | $\frac{x}{m}$=$\frac{n}{y}$ |
分析 根据比例的性质,把每一个选项中的比例改写成乘积形式的等式,与前一个等式mx=ny一致的,就说明正确,否则就是错误.
解答 解:A、由$\frac{x}{y}=\frac{n}{m}$可得mx=ny,符合mx=ny,所以正确;
B、由$\frac{x}{y}=\frac{m}{n}$可得my=nx,不符合mx=ny,所以错误;
C、由$\frac{x}{m}=\frac{y}{n}$可得my=nx,不符合mx=ny,所以错误;
D、由$\frac{x}{m}=\frac{n}{y}$可得mn=xy,不符合mx=ny,所以错误.
故选:A.
点评 此题主要考查比例性质的运用,熟记“在比例里,两外项的积等于两内项的积”是解题关键.

练习册系列答案
相关题目
4. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )| A. | ∠A=∠1+∠2 | B. | 3∠A=2∠1+∠2 | C. | 2∠A=∠1+∠2 | D. | 3∠A=2(∠1+∠2) |
5.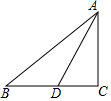 如图,在Rt△ABC中,∠ACB=90°,AD是BC边上的中线,如果AD=BC,那么tan∠B的值是( )
如图,在Rt△ABC中,∠ACB=90°,AD是BC边上的中线,如果AD=BC,那么tan∠B的值是( )
 如图,在Rt△ABC中,∠ACB=90°,AD是BC边上的中线,如果AD=BC,那么tan∠B的值是( )
如图,在Rt△ABC中,∠ACB=90°,AD是BC边上的中线,如果AD=BC,那么tan∠B的值是( )| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
 如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论中正确的结论有①③④.
如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论中正确的结论有①③④.