题目内容
已知平面直角坐标系中A(1,2),B(-1,3),C(m,n),D(m+1,n-1)可以构成一个平行四边形,求C,D两点的坐标.
考点:平行四边形的判定,坐标与图形性质
专题:
分析:首先求得直线AB和直线CD的斜率,比较后发现不相等,从而得到二者不平行,只能平分,根据中点坐标公式列出有关m、n的方程组求得m、n的值即可求得C、D两点的坐标.
解答:解:由已知得kAB=
=-
,
kCD=
=-1,
∵kAB≠kCD,
∴AB与CD不平行,
又∵四边形ABCD是平行四边形,
∴AB与CD是平互四边形的两条对角线,
∴对角线互相平分,
∴由中点坐标公式得:
∴
,
∴C(-
,3),D(
,2).
| 3-2 |
| -1-1 |
| 1 |
| 2 |
kCD=
| n-1-n |
| m+1-m |
∵kAB≠kCD,
∴AB与CD不平行,
又∵四边形ABCD是平行四边形,
∴AB与CD是平互四边形的两条对角线,
∴对角线互相平分,
∴由中点坐标公式得:
|
∴
|
∴C(-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了平行四边形的性质、坐标与图形的性质的知识,解题的关键是求得AB和CD的斜率后发现二者不平行,难度较大.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
二元一次方程
x-y=6有无数多个解,下列四对值中不是该方程的解的是( )
| 1 |
| 2 |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
小明说
为方程ax+by=10的解,小惠说
为方程ax+by=10的解.两人谁也不能说服对方,如果你想让他们的解都正确,则需要添加的条件是( )
|
|
| A、a=12,b=10 |
| B、a=9,b=10 |
| C、a=10,b=11 |
| D、a=10,b=10 |
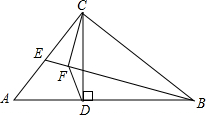 如图,在△ABC中,∠ACB=90°,CD⊥AB于D,E是AC上一点,CF⊥BE于F,求证:EB•DF=AE•BD.
如图,在△ABC中,∠ACB=90°,CD⊥AB于D,E是AC上一点,CF⊥BE于F,求证:EB•DF=AE•BD.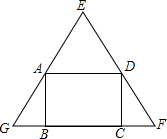 矩形ABCD的四个顶点在正△EFG的边上,已知△EFG的边长为2,记矩形ABCD的面积为S,AB边长为x,求S关于x的函数表达式和自变量的取值范围.
矩形ABCD的四个顶点在正△EFG的边上,已知△EFG的边长为2,记矩形ABCD的面积为S,AB边长为x,求S关于x的函数表达式和自变量的取值范围.