题目内容
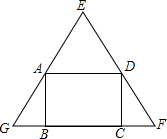矩形ABCD的四个顶点在正△EFG的边上，已知△EFG的边长为2，记矩形ABCD的面积为S，AB边长为x，求S关于x的函数表达式和自变量的取值范围．考点：相似三角形的判定与性质,等边三角形的性质,矩形的性质
专题：
分析：由等边三角形的性质可得∠G=60°，所以GB=ABtan60°=
x，同理CF=CDtan60°=
x，所以BC=GF-GB-CF=2-2
x，所以可表示出S，再由A点最多到E点，所以AB小于△EFG的高，可求得其取值范围．
| 3 |
| 3 |
| 3 |
解答：解：因为△EFG为正三角形，
所以∠G=60°，
所以GB=ABtan60°=
x，同理CF=CDtan60°=
x，
所以BC=GF-GB-CF=2-2
x，
所以S=AB×BC=x（2-2
x）=2x-2
x2，
又因为0＜BC＜BF，
所以0＜2-2
x＜2，
可求得：0＜x＜
，
所以S关于x的函数表达式为：S=2x-2
x2，自变量的取值范围：0＜x＜
．
所以∠G=60°，
所以GB=ABtan60°=
| 3 |
| 3 |
所以BC=GF-GB-CF=2-2
| 3 |
所以S=AB×BC=x（2-2
| 3 |
| 3 |
又因为0＜BC＜BF，
所以0＜2-2
| 3 |
可求得：0＜x＜
| 3 |
所以S关于x的函数表达式为：S=2x-2
| 3 |
| 3 |
点评：本题主要考查等边三角形的性质，解题的关键是利用三角函数表示出BC的长度．
练习册系列答案
阅读快车系列答案
相关题目
要使代数式7-3x的值小于-2，则x的取值范围是（ ）
| A、x＞3 | ||
| B、x＜3 | ||
| C、x＞-3 | ||
D、x＞
|
在△ABC中，tanA=
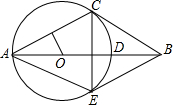
在四边形ABCD，AC与BD相交于点E，AC⊥AB，BD⊥CD，S△EBC=16，S△AED=8．求：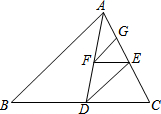
如图，AD是△ABC的中线，E是AC的中点，F是AD的中点，G是AE的中点，若△AFG的面积是2，则△ABC的面积是
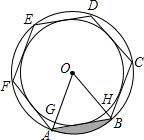如图，两个同心圆的圆心为O，正六边形ABCDEF的顶点在大圆上，六条边分别与小圆相切，大圆的半径OA、OB分别与小圆相交于点G、H，正六边形的边长为2a．