题目内容
(本题满分8分)
如图4,AB是圆O的直径,作半径OA的垂直平分线,交圆O于C、D两点,垂足为H,联结BC、BD.

(1)求证:BC=BD;
(2)已知CD=6,求圆O的半径长.
(1)证明见解析;
(2)r=2 .
.
【解析】
试题分析:由垂径定理可得CH=DH,从而BC=BD;
(2)连接OC,由已知则有OH= OC,CH=3,在Rt△CHO中利用勾股定理即可得半径长.
OC,CH=3,在Rt△CHO中利用勾股定理即可得半径长.
试题解析:(1)∵AB是圆O的直径,且AB⊥CD,∴CH=DH,∴BC=BD.
(2)连接OC.
∵CD平分OA,设圆O的半径为r,则OH= r,
r,
∵CD=6,∴CH= CD=3,
CD=3,
∵∠CHO=90°,∴OH2+CH2=CO2,
∴( r)2+32=r2,∴r=2
r)2+32=r2,∴r=2 .
.
考点:1、垂径定理;2、勾股定理.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
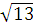 ,则点P的坐标为 .
,则点P的坐标为 .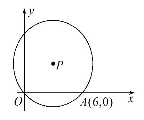
 (k>0)刻画(如图所示).
(k>0)刻画(如图所示).

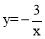 的图象上,且x1<x2<0<x3,则y1、y2、y3的大小关系是( )
的图象上,且x1<x2<0<x3,则y1、y2、y3的大小关系是( )
 +1,以下对其描述正确的是
+1,以下对其描述正确的是