题目内容
8.已知△ABC的面积为8,AB=AC,tanC=2,则AC的长为( )| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
分析 作△ABC的高AD,垂足为D,然后根据等腰三角形的性质、解直角三角函数、三角形的面积公式及勾股定理即可求得.
解答 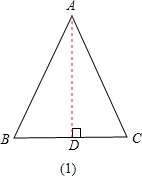 解:如图,作△ABC的高AD,垂足为D,
解:如图,作△ABC的高AD,垂足为D,
∵AB=AC,
∴BD=DC=$\frac{1}{2}$BC,
∵tanC=2,
∴$\frac{AD}{CD}$=2,
∴DC=$\frac{1}{2}$AD,
∴BC=CD,
∵△ABC的面积为8,
∴$\frac{1}{2}$BC•AD=8,
∴BC=AD=4,
∴CD=2,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=2$\sqrt{5}$.
故选B.
点评 本题考查了等腰三角形的性质、三角形的面积公式及勾股定理,解题的关键是求得AD=BC,根据买家从而求出AD、DC的值.

练习册系列答案
相关题目
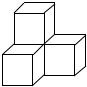 如图是由4个完全相同的小正方体组成的立体图形,它的左视图是( )
如图是由4个完全相同的小正方体组成的立体图形,它的左视图是( )