题目内容
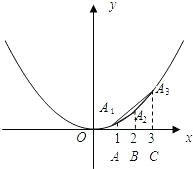
 如图,A1、A2、A3是抛物线y=ax2( a>0)上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C.A1、A2、A3三点的横坐标为连续整数n-1、n、n+1,则线段CA2的长为
如图,A1、A2、A3是抛物线y=ax2( a>0)上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C.A1、A2、A3三点的横坐标为连续整数n-1、n、n+1,则线段CA2的长为
- A.a
- B.2a
- C.n
- D.n-1
A
分析:根据题意知:A1B1∥A2B2∥A3B3,B1B2=B2B3,得到A1C=CA3,求出B2C的长,把x=n代入解析式求出A2B2的长,相减即可得到答案.
解答:根据题意知:A1B1∥A2B2∥A3B3,B1B2=B2B3,
∴A1C=CA3,
∴B2C= (A1B1+A3B3),
(A1B1+A3B3),
= [a(n-1)2+a(n+1)2],
[a(n-1)2+a(n+1)2],
=an2+a,
∵A2B2=an2,
CA2=B2C-A2B2=a.
故答案为:a.
点评:本题主要考查了梯形的中位线定理,二次函数图象上点的坐标特征等知识点,解此题的关键是求出B2C的长.
分析:根据题意知:A1B1∥A2B2∥A3B3,B1B2=B2B3,得到A1C=CA3,求出B2C的长,把x=n代入解析式求出A2B2的长,相减即可得到答案.
解答:根据题意知:A1B1∥A2B2∥A3B3,B1B2=B2B3,
∴A1C=CA3,
∴B2C=
 (A1B1+A3B3),
(A1B1+A3B3),=
 [a(n-1)2+a(n+1)2],
[a(n-1)2+a(n+1)2],=an2+a,
∵A2B2=an2,
CA2=B2C-A2B2=a.
故答案为:a.
点评:本题主要考查了梯形的中位线定理,二次函数图象上点的坐标特征等知识点,解此题的关键是求出B2C的长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是否存在最大值?若存在,请求出此值;若不存在,请说明理由.
是否存在最大值?若存在,请求出此值;若不存在,请说明理由. 如图,A1、A2、A3是抛物线y=ax2( a>0)上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C.A1、A2、A3三点的横坐标为连续整数n-1、n、n+1,则线段CA2的长为( )
如图,A1、A2、A3是抛物线y=ax2( a>0)上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C.A1、A2、A3三点的横坐标为连续整数n-1、n、n+1,则线段CA2的长为( )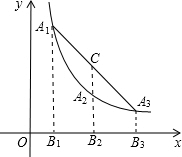 如图,A1、A2、A3是双曲线y=
如图,A1、A2、A3是双曲线y= 18、如图,A1、A2、A3是抛物线y=ax2( a>0)上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C,A1、A2、A3三点的横坐标为连续整数n-1、n、n+1,则线段CA2的长为
18、如图,A1、A2、A3是抛物线y=ax2( a>0)上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C,A1、A2、A3三点的横坐标为连续整数n-1、n、n+1,则线段CA2的长为 (2008•淮北模拟)如图,a1,a2,a3,a4的大小关系是( )
(2008•淮北模拟)如图,a1,a2,a3,a4的大小关系是( )