题目内容

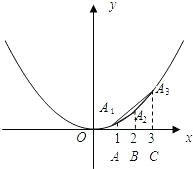
18、如图，A1、A2、A3是抛物线y=ax2（ a＞0）上的三点，A1B1、A2B2、A3B3分别垂直于x轴，垂足为B1、B2、B3，直线A2B2交线段A1A3于点C，A1、A2、A3三点的横坐标为连续整数n-1、n、n+1，则线段CA2的长为
a
．
分析：根据已知条件求出各点的横坐标和纵坐标，推出各线段的长度，继而推出CB2为梯形的中位线，根据梯形中位线的性质即可求出CB2的的长度，就可推出CA2的长
解答：解：∵A1B1、A2B2、A3B3分别垂直于x轴，垂足为B1、B2、B3
∴A1B1∥A2B2∥A3B3，A1N⊥A1B1⊥A2B2⊥A3B3
∵A1、A2、A3三点的横坐标为连续整数n-1、n、n+1，A1、A2、A3是抛物线y=ax2
∴B1B2=B2B3，
∴B2C为梯形A1A3B3B1的中位线
∴A1、A2、A3三点的纵坐标为a（n-1）2，an2，a（n+1）2
∴CB2=a（n2+1）
∴CA2=a（n2+1）-an2=a
故答案为a
点评：本题主要考察抛物线的性质，梯形的有关定理和性质，本题关键在于求出各点坐标的表达式，以此推出各线段的长度．
练习册系列答案
相关题目
（1）如图，A1，A2，A3是抛物线y=
1
4
x2图象上的三点，若A1，A2，A3三点的横坐标从左至右依次为1，2，3．求△A1A2A3的面积．
（2）若将（1）问中的抛物线改为y=
1
4
x2-
1
2
x+2和y=ax2+bx+c（a＞0），其他条件不变，请分别直接写出两种情况下△A1A2A3的面积．
（3）现有一抛物线组：y1=
1
2
x2-
1
3
x；y2=
1
6
x2-
1
12
x；y3=
1
12
x2-
1
25
x；y4=
1
20
x2-
1
42
x；y5=
1
30
x2-
1
63
x；…依据变化规律，请你写出抛物线组第n个式子yn的函数解析式；现在x轴上有三点A（1，0），B（2，0），C（3，0）．经过A，B，C向x轴作垂线，分别交抛物线组y1，y2，y3，…，yn于A1，B1，C1；A2，B2，C2；A3，B3，C3；…；An，Bn，Cn．记S△A1B1C1为S1，S△A2B2C2为S2，…，S△AnBnCn为Sn，试求S1+S2+S3+…+S10的值．
（4）在（3）问条件下，当n＞10时有Sn-10+Sn-9+Sn-8+…Sn的值不小于
11
242
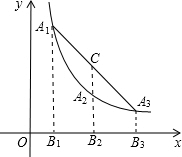，请探求此条件下正整数n精英家教网是否存在最大值？若存在，请求出此值；若不存在，请说明理由．
精英家教网如图，A1、A2、A3是抛物线y=ax2（ a＞0）上的三点，A1B1、A2B2、A3B3分别垂直于x轴，垂足为B1、B2、B3，直线A2B2交线段A1A3于点C．A1、A2、A3三点的横坐标为连续整数n-1、n、n+1，则线段CA2的长为（　　）
A、aB、2aC、nD、n-1
精英家教网如图，A1、A2、A3是双曲线y=
6x
（x＞0）上的三点，A1B1、A2B2、A3B3都垂直于x轴，垂足分别为B1、B2、B3，直线A2B2交线段A1A3于点C，A1、A2、A3三点的横坐标分别为2、4、6，则线段CA2的长为
 
．
（2008•淮北模拟）如图，a1，a2，a3，a4的大小关系是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网