题目内容
20.阅读下列解题过程:$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{1×(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3})^{2}-(\sqrt{2})^{2}}$=$\sqrt{3}$-$\sqrt{2}$
$\frac{1}{\sqrt{4}+\sqrt{3}}$=$\frac{1×(\sqrt{4}-\sqrt{3})}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$=$\frac{\sqrt{4}-\sqrt{3}}{(\sqrt{4})^{2}-(\sqrt{3})^{2}}$=2-$\sqrt{3}$
请回答下列问题:
(1)认真观察一面的解答过程,直接写出:
$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$.(n为自然数,n≥1)
(2)已知:x=$\frac{\sqrt{2}-1}{\sqrt{2}+1}$,y=$\frac{\sqrt{2}+1}{\sqrt{2}-1}$,求2x2+7xy-2y2.
分析 (1)把$\frac{1}{\sqrt{n+1}+\sqrt{n}}$分母有理化即可;
(2)先利用分母有理化得到x=3-2$\sqrt{2}$,x=3+2$\sqrt{2}$,则易得x+y=6,x-y=-4$\sqrt{2}$,xy=1,然后把原式变形为2(x+y)(x-y)+7xy,再利用整体代入的方法计算.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\frac{1×(\sqrt{n+1}-\sqrt{n})}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1})^{2}-(\sqrt{n})^{2}}$=$\sqrt{n+1}$-$\sqrt{n}$;
故答案为$\sqrt{n+1}$-$\sqrt{n}$;
(2)∵x=($\sqrt{2}$-1)2=3-2$\sqrt{2}$,x=($\sqrt{2}$+1)2=3+2$\sqrt{2}$,
∴x+y=6,x-y=-4$\sqrt{2}$,xy=1,
∴原式=2(x+y)(x-y)+7xy
=2×6×(-4$\sqrt{2}$)+7×1
=7-48$\sqrt{2}$.
点评 本题考查了分母有理化:分母有理化是指把分母中的根号化去.分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.在△ABC中,AB=AC,AD是BC边上的高,若AB=5cm,BC=6cm,则AD的长是( )
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
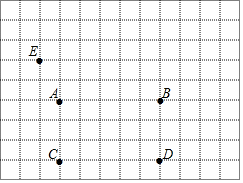 某区进行课堂教学改革,将学生分成5个学习小组,采取团团坐的方式.如图,这是某校八(1)班教室简图,点A、B、C、D、E分别代表五个学习小组的位置.已知A点的坐标为(-1,3).
某区进行课堂教学改革,将学生分成5个学习小组,采取团团坐的方式.如图,这是某校八(1)班教室简图,点A、B、C、D、E分别代表五个学习小组的位置.已知A点的坐标为(-1,3).