题目内容
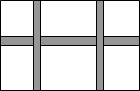 如图所示,在一块长为30米,宽为20米的矩形场地中间要设计一横二竖的等宽的、供居民散步的小路,其余种草.若要使小路总面积为68平方米,设小路的宽为x米,则可列方程为
如图所示,在一块长为30米,宽为20米的矩形场地中间要设计一横二竖的等宽的、供居民散步的小路,其余种草.若要使小路总面积为68平方米,设小路的宽为x米,则可列方程为考点:由实际问题抽象出一元二次方程
专题:几何图形问题
分析:本题可根据关键语“小路的面积是68平方米”,把小路移到一起正好构成一个矩形,矩形的长和宽分别是(30-2x)米和(20-x)米,列方程即可求解.
解答:解:设小路的宽应是x米,则剩下草地总长为:(30-2x)米,总宽为:(20-x)米,
由题意得(30-2x)(20-x)=30×20-68,
故答案为:(30-2x)(20-x)=30×20-68.
由题意得(30-2x)(20-x)=30×20-68,
故答案为:(30-2x)(20-x)=30×20-68.
点评:考查了由实际问题抽象出一元二次方程的知识,解题的关键是找到等量关系.

练习册系列答案
相关题目
设x是有理数,那么下列各式中一定表示正数的是( )
| A、2014x |
| B、x+2014 |
| C、|2014x| |
| D、|x|+2014 |
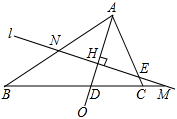 在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于D,H为AO上一动点,直线l⊥AO于H,交AB、AC、BC于N、E、M,求∠ABC和∠EMB的关系.
在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于D,H为AO上一动点,直线l⊥AO于H,交AB、AC、BC于N、E、M,求∠ABC和∠EMB的关系. 如图,正方形ABCD的边长为6,E为BC上一点,CE=2BE,将△ABE沿AE折叠得到△AFE,连接DF,则线段DF的长度是多少?
如图,正方形ABCD的边长为6,E为BC上一点,CE=2BE,将△ABE沿AE折叠得到△AFE,连接DF,则线段DF的长度是多少?