题目内容
已知函数y=x2+px+q的图象与x轴两个交点的坐标分别是(x1,0)(x2,0),若x1+x2=6,x12+x22=20,求p、q的值.
考点:抛物线与x轴的交点
专题:
分析:根据一元二次方程根与系数的关系已知x1+x2=6即可得到p的值,再由x1+x2=6,x12+x22=20求得x1x2即可.
解答:解:∵函数y=x2+px+q的图象与x轴两个交点的坐标分别是(x1,0)(x2,0),
∴x1、x2为方程x2+px+q=0的两根.
∴p=(x1+x2)=-6.
x1x2=
[(x1+x2)2-(x12+x22)]=
(36-20)=8.
∵△=p2-4q=(-6)2-4×8=4>0.
∴方程有实数根,
∴p=-6,q=8.
∴x1、x2为方程x2+px+q=0的两根.
∴p=(x1+x2)=-6.
x1x2=
| 1 |
| 2 |
| 1 |
| 2 |
∵△=p2-4q=(-6)2-4×8=4>0.
∴方程有实数根,
∴p=-6,q=8.
点评:本题考查了抛物线和x轴交点的问题,解答此题要知道一元二次方程根的情况与判别式△的关系和一元二次方程根与系数的关系.

练习册系列答案
相关题目
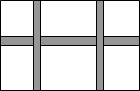 如图所示,在一块长为30米,宽为20米的矩形场地中间要设计一横二竖的等宽的、供居民散步的小路,其余种草.若要使小路总面积为68平方米,设小路的宽为x米,则可列方程为
如图所示,在一块长为30米,宽为20米的矩形场地中间要设计一横二竖的等宽的、供居民散步的小路,其余种草.若要使小路总面积为68平方米,设小路的宽为x米,则可列方程为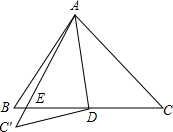 如图所示,AD是△ABC的中线,现把△ADC沿AD翻折,得△ADC′,AC′与DB交于点E,则△ABE和△C′ED的面积之比为
如图所示,AD是△ABC的中线,现把△ADC沿AD翻折,得△ADC′,AC′与DB交于点E,则△ABE和△C′ED的面积之比为