题目内容
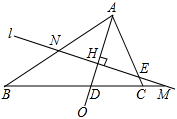 在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于D,H为AO上一动点,直线l⊥AO于H,交AB、AC、BC于N、E、M,求∠ABC和∠EMB的关系.
在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于D,H为AO上一动点,直线l⊥AO于H,交AB、AC、BC于N、E、M,求∠ABC和∠EMB的关系.考点:三角形内角和定理,三角形的外角性质
专题:分类讨论
分析:分①点E在AC上,根据等腰三角形三线合一的性质可得∠ANH=∠AEH,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EMB+∠CEM=∠ACB,∠EMB+∠B=∠ANH,然后整理即可得解;②点E、C、M重合时,∠EMB不存在;③点E在AC的延长线上时,根据等腰三角形三线合一的性质可得∠ANH=∠AEH,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠B+∠BMN=∠ANH,∠AEH+∠EMC=∠ACB,然后整理即可得解.
解答: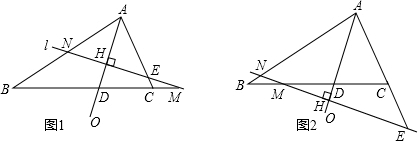 解:①如图1,点E在AC上,
解:①如图1,点E在AC上,
∵直线l⊥AO,AO是∠BAC的平分线,
∴∠ANH=∠AEH,
∵∠EMB+∠CEM=∠ACB,∠EMB+∠B=∠ANH,∠CEM=∠AEH(对顶角相等),
∴∠ACB-∠EMB=∠EMB+∠B,
∴∠ACB-∠B=2∠EMB,
∵∠ACB=2∠B,
∴∠ACB-∠B=∠B,
∴∠B=2∠EMB;
②点E、C、M重合时,∠EMB不存在;
③如图2,点E在AC的延长线上时,同①可得,∠ANH=∠AEH,
∠B+∠BMN=∠ANH,∠AEH+∠EMC=∠ACB,
∴∠B+∠BMN=∠ACB-∠EMC,
∴∠ACB-∠B=∠BMN+∠EMC,
∵∠ACB=2∠B,∠BMN=∠CME=180°-∠EMB,
∴∠B=2(180°-∠EMB),
∴∠EMB=180°-
∠B.
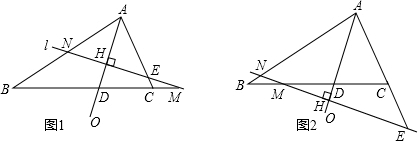 解:①如图1,点E在AC上,
解:①如图1,点E在AC上,∵直线l⊥AO,AO是∠BAC的平分线,
∴∠ANH=∠AEH,
∵∠EMB+∠CEM=∠ACB,∠EMB+∠B=∠ANH,∠CEM=∠AEH(对顶角相等),
∴∠ACB-∠EMB=∠EMB+∠B,
∴∠ACB-∠B=2∠EMB,
∵∠ACB=2∠B,
∴∠ACB-∠B=∠B,
∴∠B=2∠EMB;
②点E、C、M重合时,∠EMB不存在;
③如图2,点E在AC的延长线上时,同①可得,∠ANH=∠AEH,
∠B+∠BMN=∠ANH,∠AEH+∠EMC=∠ACB,
∴∠B+∠BMN=∠ACB-∠EMC,
∴∠ACB-∠B=∠BMN+∠EMC,
∵∠ACB=2∠B,∠BMN=∠CME=180°-∠EMB,
∴∠B=2(180°-∠EMB),
∴∠EMB=180°-
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,等腰三角形三线合一的性质,难点在于分情况讨论.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
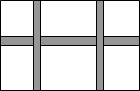 如图所示,在一块长为30米,宽为20米的矩形场地中间要设计一横二竖的等宽的、供居民散步的小路,其余种草.若要使小路总面积为68平方米,设小路的宽为x米,则可列方程为
如图所示,在一块长为30米,宽为20米的矩形场地中间要设计一横二竖的等宽的、供居民散步的小路,其余种草.若要使小路总面积为68平方米,设小路的宽为x米,则可列方程为 如图,在正方形ABCD中,AB=2cm,对角线AC、BD交于点O,点E以一定的速度从A向B移动,点F以相同的速度从B向C移动,连结OE、OF、EF.
如图,在正方形ABCD中,AB=2cm,对角线AC、BD交于点O,点E以一定的速度从A向B移动,点F以相同的速度从B向C移动,连结OE、OF、EF.