题目内容
 如图,△ABC为等边三角形,D是BC边上的一点,△ABD经过旋转后到达△ACE的位置.
如图,△ABC为等边三角形,D是BC边上的一点,△ABD经过旋转后到达△ACE的位置.(1)请说出旋转中心,旋转方向以及旋转角度;
(2)请找出AB.AD旋转后的对应线段;
(3)若∠BAD=25°,求∠AEC度数.
考点:旋转的性质
专题:
分析:(1)利用定义即可解决问题.
(2)利用定义即可解决问题.
(3)根据旋转变换的性质得到△ABD≌△ACE,借助三角形内角和定理即可解决问题.
(2)利用定义即可解决问题.
(3)根据旋转变换的性质得到△ABD≌△ACE,借助三角形内角和定理即可解决问题.
解答:解:(1)由题意知:
点A为旋转中心,旋转方向为顺时针,旋转角为60°.
(2)AB、AD的对应线段分别为AC、AE.
(3)∵△ABC为等边三角形,
∴∠B=60°;
又∵∠BAD=25°,
∴∠ADB=180°-25°-60°=95°;
由题意知△ABD≌△ACE,
∴∠AEC=∠ADB=95°,
即∠AEC度数为95°.
点A为旋转中心,旋转方向为顺时针,旋转角为60°.
(2)AB、AD的对应线段分别为AC、AE.
(3)∵△ABC为等边三角形,
∴∠B=60°;
又∵∠BAD=25°,
∴∠ADB=180°-25°-60°=95°;
由题意知△ABD≌△ACE,
∴∠AEC=∠ADB=95°,
即∠AEC度数为95°.
点评:该题考查了旋转变换的定义、性质及其应用问题;解题的关键是充分利用旋转变换的特点,灵活解题.

练习册系列答案
相关题目
一座山峰,从底端开始每升高100米气温下降0.6℃.小明从山峰底端出发向上攀登,当他到达300米高处时,此时的气温相比底端气温下降( )
| A、-1.8℃ | B、1.8℃ |
| C、-1.2℃ | D、1.2℃ |
 如图所示根据图中给出的零件的数据,求∠α的度数.
如图所示根据图中给出的零件的数据,求∠α的度数.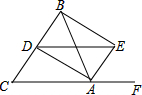 如图,△ABC中,AB=AC,F是CA延长线上一点,AD、AE分别平分∠BAC和∠BAF,BE⊥AE,说明:AB=DE.
如图,△ABC中,AB=AC,F是CA延长线上一点,AD、AE分别平分∠BAC和∠BAF,BE⊥AE,说明:AB=DE.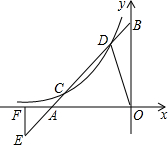 已知直线y=x+3与x轴、y轴分别交于A,B点,与y=
已知直线y=x+3与x轴、y轴分别交于A,B点,与y=