题目内容
17.解方程:|x+1|+|x-3|=4.分析 求出x+1=0和x-3=0的解,分为5种情况,再每种情况去掉绝对值符号后求出每个方程的解即可.
解答 解:①当x=-1时,0+4=4;
②当x=3时,4+0=4;
③当x<-1时,-x-1+3-x=4,
解得:x=-1,
此时不符合x<-1;
④当-1<x<3时,x+1+3-x=4,
4=4;
⑤当x>3时,x+1+x-3=4,
解得:x=3,
此时不符合x>3;
所以原方程的解为x=-1或x=3.
点评 本题考查了绝对值和一元一次方程的应用,能求出符合条件的所有情况是解此题的关键.

练习册系列答案
相关题目
9.数a与3的和的2倍,可列代数式为( )
| A. | 2(a+3) | B. | 2a+3 | C. | 3a+2 | D. | 3(a+2) |
7.下列从左边到右边的变形,属于因式分解的是( )
| A. | (x+1)(x-1)=x2-1 | B. | x2-2x+1=x(x•2)+a | C. | (a-b)(b-a)=(b-a)(a-b) | D. | (x-1)(x-3)+1=(x-2)2 |
 把下列各数在数轴上表示出来.-2$\frac{1}{2}$,0,-1,1,|-3$\frac{1}{2}$|
把下列各数在数轴上表示出来.-2$\frac{1}{2}$,0,-1,1,|-3$\frac{1}{2}$|
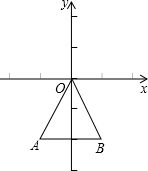 如图,△OAB三个顶点的坐标分别为O(0,0)、A(-1,-2)、B(1,-2),以B点为位似中心将△OAB放大2倍,求放大后的三角形各顶点的坐标.(提示:分两种情况)
如图,△OAB三个顶点的坐标分别为O(0,0)、A(-1,-2)、B(1,-2),以B点为位似中心将△OAB放大2倍,求放大后的三角形各顶点的坐标.(提示:分两种情况)