题目内容
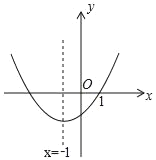
【题目】在平面直角坐标系中，二次函数y＝ax2+bx+c（a≠0）的图象如图所示，现给以下结论：①abc＜0；②c+2a＜0；③9a﹣3b+c＝0；④a﹣b≥m（am+b）（m为实数）；⑤4ac﹣b2＜0．其中错误结论的个数有（ ）
A.1个B.2个C.3个D.4个
【答案】A
【解析】
由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
解：①由抛物线可知：a＞0，c＜0，
对称轴x＝﹣
＜0，
∴b＞0，
∴abc＜0，故①正确；
②由对称轴可知：﹣＝﹣1，
∴b＝2a，
∵x＝1时，y＝a+b+c＝0，
∴c+3a＝0，
∴c+2a＝﹣3a+2a＝﹣a＜0，故②正确；
③（1，0）关于x＝﹣1的对称点为（﹣3，0），
∴x＝﹣3时，y＝9a﹣3b+c＝0，故③正确；
④当x＝﹣1时，y的最小值为a﹣b+c，
∴x＝m时，y＝am2+bm+c，
∴am2+bm+c≥a-b+c，
即a﹣b≤m（am+b），故④错误；
⑤抛物线与x轴有两个交点，
∴△＞0，
即b2﹣4ac＞0，
∴4ac﹣b2＜0，故⑤正确；
故选：A．
名校课堂系列答案
【题目】随着生活节奏的加快以及智能手机的普及，外卖点餐逐渐成为越来越多用户的餐饮消费习惯．由此催生了一批外卖点餐平台，已知某外卖平台的送餐费用与送餐距离有关（该平台只给5千米范围内配送），为调査送餐员的送餐收入，现从该平台随机抽取80名点外卖的用户进行统计，按送餐距离分类统计结果如下表：
送餐距离x（千米） | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
（1）从这80名点外卖的用户中任取一名用户，该用户的送餐距离不超过3千米的概率为 ；
（2）以这80名用户送餐距离为样本，同一组数据取该小组数据的中间值（例如第二小组（1＜x ≤2）的中间值是1.5），试估计利用该平台点外卖用户的平均送餐距离；
（3）若该外卖平台给送餐员的送餐费用与送餐距离有关，不超过2千米时，每份3元；超过2千米但不超4千米时，每份5元；超过4千米时，每份9元． 以给这80名用户所需送餐费用的平均数为依据，若送餐员一天的目标收入不低于150元，试估计一天至少要送多少份外卖？
【题目】为了强化学生的环保意识，某校团委在全校举办了“保护环境，人人有责”知识竞赛活动，初、高中根据初赛成绩，各选出5名选手组成初中代表队和高中代表队进行复赛，两个队学生的复赛成绩（满分10分）如图所示：
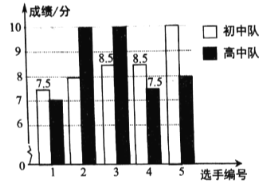
（1）根据图示填写下表：
平均分 | 中位数 | 众数 | 方差 | |
初中队 | 8.5 | 0.7 | ||
高中队 | 8.5 | 10 |
（2）小明同学说：“这次复赛我得了8分，在我们队中排名属中游偏下！”小明是初中队还是高中队的学生？为什么？
（3）结合两队成绩的平均分、中位数和方差，分析哪个对的复赛成绩较好．
