题目内容
【题目】请认真阅读下面的数学探究,并完成所提出的问题.
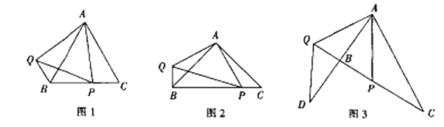
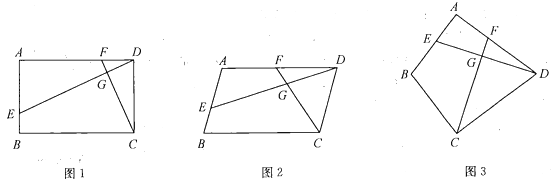
(1)探究1:如图1,在边长为![]() 的等边三角形
的等边三角形![]() 中,
中,![]() 是
是![]() 边上任意一点,连接
边上任意一点,连接![]() ,将
,将![]() 绕点
绕点![]() 按顺时针方向旋转至
按顺时针方向旋转至![]() 处,连接
处,连接![]() ,求
,求![]() 面积的最小值.
面积的最小值.
(2)探究2:如图2,若![]() 是腰长为
是腰长为![]() 的等腰直角三角形,
的等腰直角三角形,![]() ,(1)中的其他条件不变,请求出此时
,(1)中的其他条件不变,请求出此时![]() 面积的最小值.
面积的最小值.
(3)探究3:如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 边上任意一点,连接
边上任意一点,连接![]() ,将
,将![]() 绕点
绕点![]() 按顺时针方向旋转至
按顺时针方向旋转至![]() 处,
处,![]() 、
、![]() 、
、![]() 三点共线,连接
三点共线,连接![]() ,求
,求![]() 的面积的最小值.
的面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)过点![]() 作
作![]() 于点
于点![]() ,可以求出
,可以求出![]() 的面积,根据
的面积,根据![]() 是等边三角形,可以得出
是等边三角形,可以得出![]() ,所以
,所以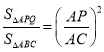 ,当点
,当点![]() 与点
与点![]() 重合时,
重合时,![]() 最小,即可求出
最小,即可求出![]() 的面积的最小值为
的面积的最小值为 .
.
(2)过点![]() 作
作![]() 于点
于点![]() ,可以求得
,可以求得![]() 的面积,易知
的面积,易知![]() ,所以
,所以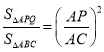 ,当点
,当点![]() 与点
与点![]() 重合时,
重合时,![]() 最小,即可求出
最小,即可求出![]() 的面积的最小值为
的面积的最小值为 .
.
(3)由已知条件可证![]() 是等边三角形,所当点
是等边三角形,所当点![]() 与点
与点![]() 重合时,
重合时,![]() 最小,即可求得
最小,即可求得![]() 的面积的最小值.
的面积的最小值.
解:(1)如图,过点![]() 作
作![]() 于点
于点![]() .
.

∵![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
由旋转的性质可知,![]() ,
,![]() ,
,
∴![]() 是等边三角形.
是等边三角形.
∵![]() 是等边三角形,∴
是等边三角形,∴![]() ,
,
∴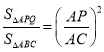 .
.
∵当点![]() 与点
与点![]() 重合时,
重合时,![]() 最小,
最小,
∴![]() 的面积的最小值为
的面积的最小值为 .
.
(2)如图,过点![]() 作
作![]() 于点
于点![]() .
.
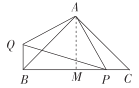
∵![]() 是腰长为
是腰长为![]() 的等腰直角三角形,
的等腰直角三角形,
∴![]() ,∴
,∴![]() ,
,![]() .
.
由旋转的性质可知,![]() ,
,![]() ,
,
∴![]() 是等腰直角三角形.
是等腰直角三角形.
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,∴
,∴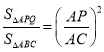 .
.
∵当点![]() 与点
与点![]() 重合时,
重合时,![]() 最小,
最小,
∴![]() 的面积的最小值为
的面积的最小值为 .
.
(3)∵在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
由旋转的性质可知,![]() ,
,![]() ,
,
∴![]() 是等边三角形.
是等边三角形.
∵当点![]() 与点
与点![]() 重合时,
重合时,![]() 最小,
最小,
∴![]() 的面积的最小值为
的面积的最小值为 .
.

练习册系列答案
相关题目