Question

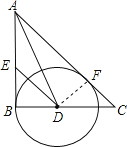
【题目】如图，在Rt△ABC中，∠B＝90°，∠BAC的平分线交BC于点D，E为AB上的一点，DE＝DC，以D为圆心，DB长为半径作⊙D，AB＝5，EB＝3．

（1）求证：AC是⊙D的切线；

（2）求线段AC的长．

Answer 1

【答案】（1）证明见解析；（2）8

【解析】

（1）过点D作DF⊥AC于F，根据切线的性质可得∠B=90°，即AB⊥BC，然后根据角平分线的性质可得DE=DF，从而证得结论；

（2）根据已知DE=DC和（1）的结论可知DF⊥AC，AB⊥BC以及半径DB=DF，得证Rt△BDE≌Rt△DCF（HL），进而得证EB=FC,再由AB=AF，可知AC=AF+FC=AB+EB=8．

解：（1）过点D作DF⊥AC于F；

∵AB为⊙D的切线，

∴∠B=90°，

∴AB⊥BC

∵AD平分∠BAC，DF⊥AC，

∴BD=DF，

∴AC与圆D相切；

（2）在△BDE和△DCF中；

∵BD=DF，DE=DC，

∴Rt△BDE≌Rt△DCF（HL），

∴EB=FC．

∵AB=AF，

∴AB+EB=AF+FC，

即AB+EB=AC，

∴AC=5+3=8．