题目内容
3. 已知二次函数y=-x2+4x.
已知二次函数y=-x2+4x.(1)写出二次函数y=-x2+4x图象的对称轴;
(2)在给定的平面直角坐标系中,画出这个函数的图象(列表、描点、连线);
(3)根据图象,写出当y<0时,x的取值范围.
分析 (1)把一般式化成顶点式即可求得;
(2)首先列表求出图象上点的坐标,进而描点连线画出图象即可.
(3)根据图象从而得出y<0时,x的取值范围.
解答 解:(1)∵y=-x2+4x=-(x-2)2+4,
∴对称轴是过点(2,4)且平行于y轴的直线x=2;
(2)列表得:
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | -5 | 0 | 3 | 4 | 3 | 0 | -5 | … |

(3)由图象可知,
当y<0时,x的取值范围是x<0或x>4.
点评 本题考查了二次函数的图象和二次函数的性质,要会利用数形结合的思想把代数和几何图形结合起来,利用二次函数的图象,从而求出y<0时,x的取值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.一元二次方程x2+4x=0的解是( )
| A. | x=-4 | B. | x1=0,x2=-4 | C. | x=4 | D. | x1=0,x2=4 |
15.某种商品经连续两次降价后价格为原来的81%,设价格平均每次下降百分率为x,则可列方程( )
| A. | (1-x)2=81% | B. | (1+x)2=81% | C. | 1-2x=81% | D. | 1+2x=81% |

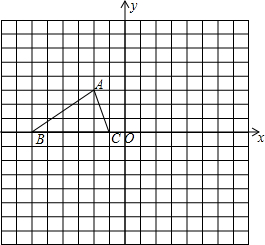 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).