题目内容
3.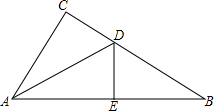 在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线交BC于D,交AB于E,DB=12cm,则CD=6cm.
在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线交BC于D,交AB于E,DB=12cm,则CD=6cm.
分析 根据直角三角形的性质得到DE=$\frac{1}{2}$BD,根据线段垂直平分线的性质得到DA=DB,证明∠CAD=∠DAB,根据角平分线的性质得到答案.
解答 解:∵DE⊥AB,∠B=30°,
∴DE=$\frac{1}{2}$BD=6,
∵DE是AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B=30°,又∠C=90°,
∴∠CAD=∠DAB,又∠C=90°,DE⊥AB,
∴DC=DE=6.
故答案为:6cm.
点评 本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.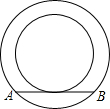 如图,两个同心圆的直径分别为6cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
如图,两个同心圆的直径分别为6cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
 如图,两个同心圆的直径分别为6cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
如图,两个同心圆的直径分别为6cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
 已知:如图,点C为AB中点,CD=BE,CD∥BE.
已知:如图,点C为AB中点,CD=BE,CD∥BE.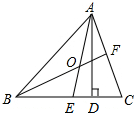 如图,在△ABC中,AD是高,AE和BF是角平分线,它们相交于点O,∠ABC=60°,∠C=70°,求∠CAD和∠AOF的度数.
如图,在△ABC中,AD是高,AE和BF是角平分线,它们相交于点O,∠ABC=60°,∠C=70°,求∠CAD和∠AOF的度数.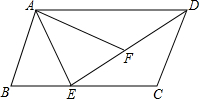 如图,在四边形ABCD中,AB=CD,AD∥BC,AB∥CD,∠B=∠AFE,EA是∠BAF的角平分线,求证:
如图,在四边形ABCD中,AB=CD,AD∥BC,AB∥CD,∠B=∠AFE,EA是∠BAF的角平分线,求证: 如图,在△ABC中,∠B=45°,∠C=60°,BC=6,求AB、AC的长(结果保留根号)
如图,在△ABC中,∠B=45°,∠C=60°,BC=6,求AB、AC的长(结果保留根号)