题目内容
已知:如图,△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE;垂足为E.
(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?
请证明你的结论.
 |
(1)证明:∵AB=AC ∴∠B=∠ACB
又因为AD是BC边上的中线
所以AD⊥BC,即∠ADB=90°
因为AE∥BC 所以∠EAC=∠ACB
所以∠B=∠EAC
∵CE⊥AE ∴∠CEA=90°
∴∠CEA=∠ADB
又AB=AC ∴△ABD≌△CAE(AAS)
(2)AB∥DE且AB=DE。
由(1)△ABD≌△CAE可得AE=BD,
又AE∥BD,所以四边形ABDE是平行四边形
所以AB∥DE且AB=DE

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目

 ,那么
,那么
 的一元二次方程
的一元二次方程  有两个不相等的实数根,求
有两个不相等的实数根,求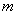 的取值范围
的取值范围 B.
B.  C.
C.  D.
D. 
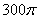 cm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径
cm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径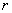 为【 】
为【 】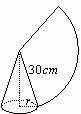
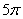 cm
cm 轴,
轴, 轴的正半轴于A,B两点,且M是AB的中点. 以OM为直径的⊙P分别交
轴的正半轴于A,B两点,且M是AB的中点. 以OM为直径的⊙P分别交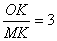 ,求∠OBA的度数;
,求∠OBA的度数;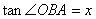 (0<
(0<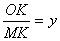 ,直接写出
,直接写出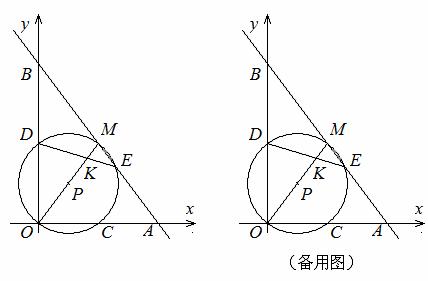
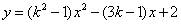 .
. 轴上,求
轴上,求 的值;
的值;