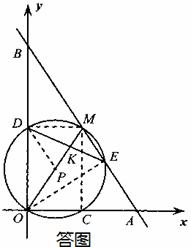
题目内容
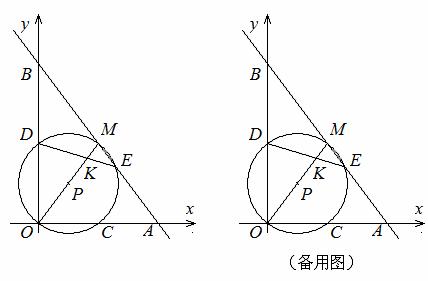
如图,在平面直角坐标系中,点M是第一象限内一点,过M的直线分别交 轴,
轴, 轴的正半轴于A,B两点,且M是AB的中点. 以OM为直径的⊙P分别交
轴的正半轴于A,B两点,且M是AB的中点. 以OM为直径的⊙P分别交 轴,
轴, 轴于C,D两点,交直线AB于点E(位于点M右下方),连结DE交OM于点K.
轴于C,D两点,交直线AB于点E(位于点M右下方),连结DE交OM于点K.
(1)若点M的坐标为(3,4),①求A,B两点的坐标; ②求ME的长;
(2)若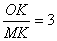 ,求∠OBA的度数;
,求∠OBA的度数;
(3)设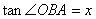 (0<
(0< <1),
<1),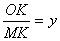 ,直接写出
,直接写出 关于
关于 的函数解析式.
的函数解析式.
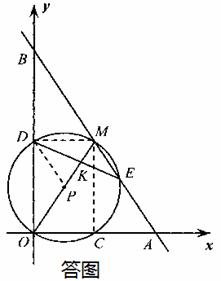 解:(1)①如答图,连接
解:(1)①如答图,连接 ,
,
∵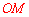 是⊙P的直径,∴
是⊙P的直径,∴ .
.
∵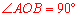 ,∴
,∴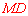 ∥
∥ ,
,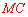 ∥
∥ .
.
∵点M是AB的中点,
∴点D是AB的中点,点C是OA的中点.
∵点M的坐标为(3,4),
∴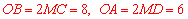 .
.
∴点B的坐标为(0,8),点A的坐标为(6,0).
②在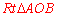 中,∵
中,∵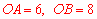 ,
,
∴由勾股定理,得 .
.
∵点M是AB的中点,∴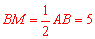 .
.
∵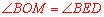 ,
, ,∴
,∴ .∴
.∴ .
.
∴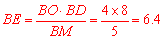 .∴
.∴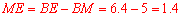 .
.
(2)如答图,连接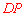 ,
,
∵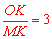 ,∴
,∴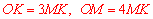 .∴
.∴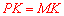 .
.
∵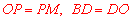 ,∴
,∴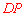 是
是 的中位线. ∴
的中位线. ∴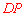 ∥
∥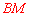 .∴
.∴
又∵ .∴
.∴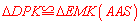 .∴
.∴ .
.
∵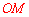 是⊙P的直径,∴
是⊙P的直径,∴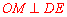 . ∴
. ∴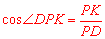 .
.
∵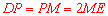 ,∴
,∴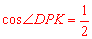 .∴
.∴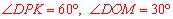 .
.
∵在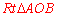 中,点M是AB的中点,∴
中,点M是AB的中点,∴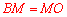 . ∴
. ∴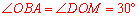 .
.
(3)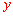 关于
关于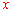 的函数解析式为
的函数解析式为 .
.
【分析】(1)①连接 ,由三角形中位线定理求得A,B两点的坐标.
,由三角形中位线定理求得A,B两点的坐标.
②要求ME的长,由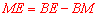 知只要求出
知只要求出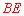 和
和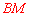 的长即可,
的长即可,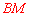 的长可由
的长可由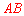 长的一半求得,而
长的一半求得,而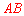 长可由勾股定理求得;
长可由勾股定理求得;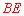 的长可由
的长可由 的对应边成比例列式求得.
的对应边成比例列式求得.
(2)连接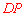 ,求得
,求得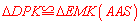 得到
得到 ,由
,由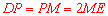 得到
得到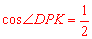 ,即
,即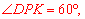 因此求得
因此求得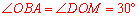 .
.
(3)如答图,连接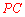 ,
,
∵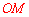 是⊙P的直径,∴
是⊙P的直径,∴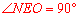 .
.
∵ (0<
(0< <1),不妨设
<1),不妨设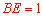 ,
,
∴在 中,
中, .
.
设 ,则
,则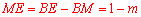 .
.
∵在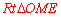 中,
中,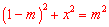 ,∴
,∴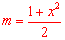 .
.
∴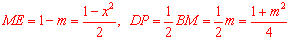 .
.
∵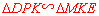 ,∴
,∴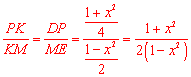 .
.
∴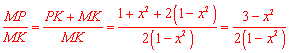 .
.
∵点P是MO的中点,∴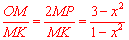 .
.
∴ .
.
∴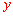 关于
关于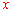 的函数解析式为
的函数解析式为 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 =
= 
 B.
B. C.
C. D.
D.
 与x轴交与A,B两点(点A在点B的左侧),与y轴交于点C. 点D和点C关于抛物线的对称轴对称,直线AD与y轴相交于点E.
与x轴交与A,B两点(点A在点B的左侧),与y轴交于点C. 点D和点C关于抛物线的对称轴对称,直线AD与y轴相交于点E.