题目内容
3.已知等腰三角形ABC的顶点A的坐标是(0,3),腰长为4,并且底边在x轴上,求点B、C的坐标.分析 根据等腰三角形是轴对称图形,其底边的垂直平分线是对称轴,可知点B、C关于y轴对称,根据AB=AC=4利用勾股定理求出OB、OC的长,即可得出点B、C的坐标.
解答  解:∵等腰三角形ABC的顶点A的坐标是(0,3),腰长为4,
解:∵等腰三角形ABC的顶点A的坐标是(0,3),腰长为4,
∴OA=3,AB=AC=4,OB=OC=$\sqrt{{4}^{2}-{3}^{2}}=\sqrt{7}$,
∵点B、C在x轴上,
∴点B、C的坐标分别是($-\sqrt{7}$,0),($\sqrt{7}$,0).
点评 本题考查了等腰三角形的性质,坐标与图形性质和勾股定理的应用,利用勾股定理得出OB、OC的长是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 下列选项中能由左图平移得到的是( )
下列选项中能由左图平移得到的是( )
 下列选项中能由左图平移得到的是( )
下列选项中能由左图平移得到的是( )| A. |  | B. |  | C. |  | D. |  |
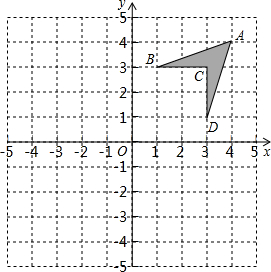 如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1)
如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1)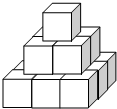 如图把14个棱长为1分米的正方体摆放在课桌上,现在想露出的表面都涂上颜色,则涂上颜色部分的面积为33平方分米.
如图把14个棱长为1分米的正方体摆放在课桌上,现在想露出的表面都涂上颜色,则涂上颜色部分的面积为33平方分米.