题目内容
2．若等腰三角形腰上的高是底边的一半，则这个等腰三角形的底角是（ ）| A． | 75°或30° | B． | 30° | C． | 15° | D． | 75°和15° |
分析 画出图形，根据直角三角形中30°角所对直角边是斜边一半即可求得∠C的大小，根据等腰三角形底角相等即可解题．
解答 解：如图，等腰三角形ABC中，AB=AC，BD是AC边上高，
∵BD⊥AC，
∴△BCD为直角三角形，
∵BC=2BD，
∴∠C=30°，
∴∠ABC=∠C=30°，
故选B．
点评 本题考查了直角三角形中30°角所对直角边是斜边一半的性质，本题中画出图形并求得∠C的大小是解题的关键．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
12．深圳是一个美丽的海滨城市，海岸线长达275000米，数据275000用科学记数法表为（ ）
| A． | 2.75×105 | B． | 27.5×104 | C． | 0.275×106 | D． | 2.75×107 |
13．抛物线y=-（x-8）2+2的顶点所在象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
17．能确定△ABC与△A1B1C1全等的是（ ）
| A． | AC=A1C1，BC=B1C1，∠B=∠B1 | B． | AC=A1C1，∠A=∠A1，∠B=∠B1 | ||
| C． | AC=B1C1，∠A=∠A1，∠B=∠B1 | D． | ∠A=∠A1，∠B=∠B1，∠C=∠C1 |
如图，AB=AC，∠A=50°，AB的垂直平分线MN交AC于点D，则∠DBC=15°．
14．下列各式中正确的是（ ）
| A． | $\sqrt{{{（-5）}^2}}$=-5 | B． | $\sqrt{8}=±2\sqrt{2}$ | C． | $\sqrt{48}=4\sqrt{3}$ | D． | ${（-\sqrt{2}）^2}$=4 |
如图，四个全等的直角三角形，直角边、斜边分别为a、b、c，一个边长为c的正方形，请用所给的图形拼成一个可以证明勾股定理的图案．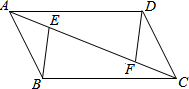
如图，在四边形ABCD中，点E、F在AC上，有下面五个论断：