题目内容
11. 如图,四个全等的直角三角形,直角边、斜边分别为a、b、c,一个边长为c的正方形,请用所给的图形拼成一个可以证明勾股定理的图案.
如图,四个全等的直角三角形,直角边、斜边分别为a、b、c,一个边长为c的正方形,请用所给的图形拼成一个可以证明勾股定理的图案.(1)画出你拼成的图形.
(2)用你所画图形证明勾股定理.
分析 根据图形可知是梯形,再根据梯形的面积等于三个直角三角形的面积的和,列式整理即可证明.
解答 解:(1)如图所示,这是一个梯形.
(2)证明:∵S梯形ABCD=S△ABE+S△AED+S△ECD,
∴$\frac{1}{2}$(a+b)•(a+b)=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$b,
∴(a+b)2=ab+c2+ab,a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
点评 本题考查了勾股定理的证明,根据图形的面积列式整理即可,题中图形答案不唯一,富有创造性,只要是根据面积可以推出勾股定理即可.

练习册系列答案
相关题目
2.若等腰三角形腰上的高是底边的一半,则这个等腰三角形的底角是( )
| A. | 75°或30° | B. | 30° | C. | 15° | D. | 75°和15° |
16.某校开展“节约每一滴水”活动,为了解开展活动的一个月以来节约用水的情况,从八年级的400名同学中选出20名同学统计了各自家庭一个月的节水情况,统计结果见下表:
请你估计这400名同学的家庭一个月节约用水的总量大约是130m3.
| 节水量/m3 | 0.2 | 0.25 | 0.3 | 0.4 | 0.5 |
| 家庭数/个 | 2 | 4 | 6 | 7 | 1 |
 五一黄金周,公司组织员工到A,B,C三地旅游,公司购买前往各地的车票种类,数量绘制成条形统计图,如图.根据图表回答:
五一黄金周,公司组织员工到A,B,C三地旅游,公司购买前往各地的车票种类,数量绘制成条形统计图,如图.根据图表回答: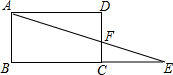 如图,点E是矩形ABCD的边BC延长线上的一点,AE交CD于F,若CF:DF=1:2,则△FCE与△ABE的面积的比是$\frac{1}{9}$.
如图,点E是矩形ABCD的边BC延长线上的一点,AE交CD于F,若CF:DF=1:2,则△FCE与△ABE的面积的比是$\frac{1}{9}$.