题目内容
10.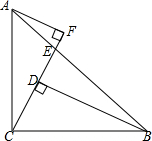 已知:如图,Rt△ABC中,AC=BC,∠ACB=90°,CF交AB于点E,BD⊥CF于点D,AF⊥CF.求证:BD=AF+DF.
已知:如图,Rt△ABC中,AC=BC,∠ACB=90°,CF交AB于点E,BD⊥CF于点D,AF⊥CF.求证:BD=AF+DF.
分析 根据全等三角形的判定定理ASA证得△AFC≌△CDB,然后由全等三角形的对应边CD=AF,BD=CF,从而求得CF=AF+DF=BD.
解答 证明:∵BD⊥CF,∠ACB=90°,AF⊥CF,
∴∠DCB+∠DBC=∠DCB+∠ACF=90°,
∴∠DBC=∠ACF,
∴∠CAF=∠BCD,
在△AFC和△CDB中,
$\left\{\begin{array}{l}{∠CAF=∠BCD}\\{AC=BC}\\{∠ACF=∠DBC}\end{array}\right.$,
∴△AFC≌△CDB(ASA),
∴CD=AF,BD=CF,
∴BD=CF=CD+DF=AF+CF.
点评 本题考查了全等三角形的判定与性质.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
20.将一根长1米的木棒,第一次截去一半,第二次截去剩下的一半,如此截下去,截至第五次,剩下的木棒长是( )米.
| A. | $\frac{1}{32}$ | B. | $\frac{1}{16}$ | C. | $\frac{15}{16}$ | D. | $\frac{31}{32}$ |
 如图,在等腰△ABC中,AB=CB,M为△ABC内一点,∠MAC+∠MCB=∠MCA=30°,求证:△ABM为等腰三角形.
如图,在等腰△ABC中,AB=CB,M为△ABC内一点,∠MAC+∠MCB=∠MCA=30°,求证:△ABM为等腰三角形.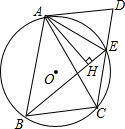 如图,已知四边形ABCD是平行四边形,边CD与⊙O相交于点E,连接AE,BE,∠DAE=∠ABE
如图,已知四边形ABCD是平行四边形,边CD与⊙O相交于点E,连接AE,BE,∠DAE=∠ABE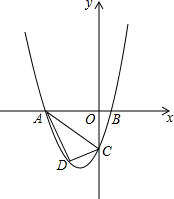 已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=4OB.
已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=4OB.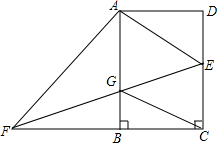 如图,在矩形ABCD中,AB=4,BC=2,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,连接EF交边AB于点G.
如图,在矩形ABCD中,AB=4,BC=2,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,连接EF交边AB于点G.