题目内容
15.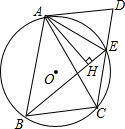 如图,已知四边形ABCD是平行四边形,边CD与⊙O相交于点E,连接AE,BE,∠DAE=∠ABE
如图,已知四边形ABCD是平行四边形,边CD与⊙O相交于点E,连接AE,BE,∠DAE=∠ABE(1)求证:AB=AC;
(2)若过点A作AH⊥BE于点H,求证:BH=CE+EH.
分析 (1)根据弦切角定理和圆周角定理证明∠ABC=∠ACB,得到答案;
(2)作AF⊥CD于F,证明△AEH≌△AEF,得到EH=EF,根据△ABH≌△ACF,得到答案.
解答 证明:(1)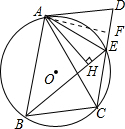 ∵AD与△ABC的外接圆⊙O恰好相切于点A,
∵AD与△ABC的外接圆⊙O恰好相切于点A,
∴∠ABE=∠DAE,又∠EAC=∠EBC,
∴∠DAC=∠ABC,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC;
(2)作AF⊥CD于F,
∵四边形ABCE是圆内接四边形,
∴∠ABC=∠AEF,又∠ABC=∠ACB,
∴∠AEF=∠ACB,又∠AEB=∠ACB,
∴∠AEH=∠AEF,
在△AEH和△AEF中,
$\left\{\begin{array}{l}{∠AHE=∠AFE}\\{∠AEH=∠AEF}\\{AE=AE}\end{array}\right.$,
∴△AEH≌△AEF,
∴EH=EF,
∴CE+EH=CF,
在△ABH和△ACF中,
$\left\{\begin{array}{l}{∠ABH=∠ACF}\\{∠AHB=∠AFC}\\{AB=AC}\end{array}\right.$,
∴△ABH≌△ACF,
∴BH=CF=CE+EH.
点评 本题考查的是切线的性质和平行四边形的性质以及全等三角形的判定和性质,运用性质证明相关的三角形全等是解题的关键,注意圆周角定理和圆内接四边形的性质的运用.

练习册系列答案
相关题目
5. 如图,在同一直角坐标系中,作出函数①y=3x2;②y=$\frac{1}{2}{x}^{2}$;③y=x2的图象,则从里到外的三条抛物线对应的函数依次是( )
如图,在同一直角坐标系中,作出函数①y=3x2;②y=$\frac{1}{2}{x}^{2}$;③y=x2的图象,则从里到外的三条抛物线对应的函数依次是( )
 如图,在同一直角坐标系中,作出函数①y=3x2;②y=$\frac{1}{2}{x}^{2}$;③y=x2的图象,则从里到外的三条抛物线对应的函数依次是( )
如图,在同一直角坐标系中,作出函数①y=3x2;②y=$\frac{1}{2}{x}^{2}$;③y=x2的图象,则从里到外的三条抛物线对应的函数依次是( )| A. | ①②③ | B. | ①③② | C. | ②③① | D. | ③②① |
6.若关于x的一元二次方程ax2+bx+1=0(a≠0)的解是x=1,则2015-a-b的值是( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
7.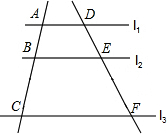 如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=( )
如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=( )
 如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=( )
如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{8}{5}$ | D. | 2 |
 如图,已知△ABC和△AEF都是等边三角形,求证:BF=CE.
如图,已知△ABC和△AEF都是等边三角形,求证:BF=CE.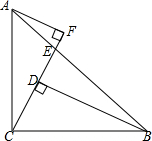 已知:如图,Rt△ABC中,AC=BC,∠ACB=90°,CF交AB于点E,BD⊥CF于点D,AF⊥CF.求证:BD=AF+DF.
已知:如图,Rt△ABC中,AC=BC,∠ACB=90°,CF交AB于点E,BD⊥CF于点D,AF⊥CF.求证:BD=AF+DF.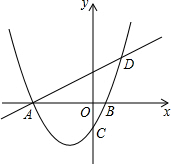 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,对称轴为直线x=-$\frac{3}{2}$,直线AD交抛物线于点D(2,3).
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,对称轴为直线x=-$\frac{3}{2}$,直线AD交抛物线于点D(2,3).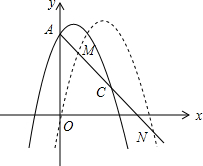 如图,已知抛物线y=-x2+3x+6交y轴于A点,点C(4,k)在抛物线上,将抛物线向右平移n个单位长度后与直线AC交于点M、N两点,且M、N关于点C成中心对称,求n的值.
如图,已知抛物线y=-x2+3x+6交y轴于A点,点C(4,k)在抛物线上,将抛物线向右平移n个单位长度后与直线AC交于点M、N两点,且M、N关于点C成中心对称,求n的值. 是方程
是方程 的一个根,那么
的一个根,那么 的值是_____.
的值是_____.