题目内容
19.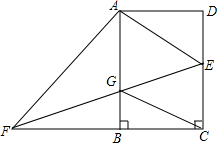 如图,在矩形ABCD中,AB=4,BC=2,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,连接EF交边AB于点G.
如图,在矩形ABCD中,AB=4,BC=2,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,连接EF交边AB于点G.(1)求证:BF=2DE;
(2)若FE平分∠AFB,连接CG,求证:四边形AGCE为菱形;
(3)当点E在边CD上移动时,△AEG能否成为等腰三角形?如果能,请直接写出线段DE的长;如果不能,请说明理由.
分析 (1)根据题意和相似三角形的判定定理证明△ABF∽△ADE,根据相似三角形的性质证明即可;
(2)证明△AFE≌△CFE,得到FA=FC,得到△AFG和△CFG,得到四边形AGCE为平行四边形,又EA=EC,根据菱形的判定定理证明结论;
(3)分AG=AE,GA=GE,EA=EG三种情况,根据全等三角形的性质、相似三角形的性质计算即可.
解答 (1)证明:∵AF⊥AE,
∴∠FAB+∠GAE=90°,又∠DAE+∠GAE=90°,
∴∠FAB=∠DAE,又∠ABF=∠ADE=90°,
∴△ABF∽△ADE,
∴$\frac{BF}{DE}$=$\frac{AB}{AD}$=2,
∴BF=2DE;
(2)证明:∵FE平分∠AFB,AF⊥AE,∠ECF=90°,
∴EA=EC,
在△AFE和△CFE中,
$\left\{\begin{array}{l}{∠AFE=∠CFE}\\{∠FAE=∠FCE}\\{FE=FE}\end{array}\right.$,
∴△AFE≌△CFE,
∴FA=FC,
∴△AFG和△CFG,
∴∠FAG=∠FCG,
∴∠DAE=∠FCG,
∴∠AED=∠GCD,
∴AE∥GC,又AG∥EC,
∴四边形AGCE为平行四边形,又EA=EC,
∴四边形AGCE为菱形;
(3)解:当四边形AGCE为菱形时,AG=AE,
设DE为x,则
(4-x)2=22+x2,
解得x=$\frac{3}{2}$;
当GA=GE时,∠GAE=∠GEA,
∴∠GAF=∠GFA,
∴GA=GF,
即G为FE的中点,
则FB=BC=2,
∴DE=$\frac{1}{2}$FB=1;
当EA=EG时,
∠EAG=∠EGA,
∴∠FAB=∠GFB,
∴△FAB∽△GFB,
∴BF2=BG•BA,
设DE=y,则AG=2y,GB=4-2y,FB=2y,
4y2=(4-2y)×4,
解得y=$\sqrt{5}$-1.
则DE=$\sqrt{5}$-1.
点评 本题考查的是矩形的性质、菱形的判定和性质、全等三角形的判定和性质、等腰三角形的性质,灵活运用性质和定理、运用方程思想和分情况讨论思想是解题的关键.

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案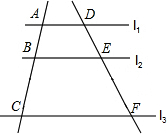 如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=( )
如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{8}{5}$ | D. | 2 |
 如图,AD是△ABC的中线,且AB=10cm,AC=6cm,求△ABD与△ACD的周长之差.
如图,AD是△ABC的中线,且AB=10cm,AC=6cm,求△ABD与△ACD的周长之差.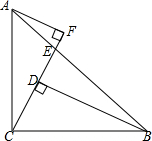 已知:如图,Rt△ABC中,AC=BC,∠ACB=90°,CF交AB于点E,BD⊥CF于点D,AF⊥CF.求证:BD=AF+DF.
已知:如图,Rt△ABC中,AC=BC,∠ACB=90°,CF交AB于点E,BD⊥CF于点D,AF⊥CF.求证:BD=AF+DF.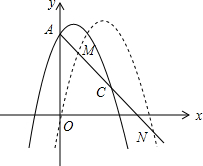 如图,已知抛物线y=-x2+3x+6交y轴于A点,点C(4,k)在抛物线上,将抛物线向右平移n个单位长度后与直线AC交于点M、N两点,且M、N关于点C成中心对称,求n的值.
如图,已知抛物线y=-x2+3x+6交y轴于A点,点C(4,k)在抛物线上,将抛物线向右平移n个单位长度后与直线AC交于点M、N两点,且M、N关于点C成中心对称,求n的值. B.
B.  C.
C.  D.
D. 
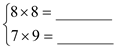 ;
;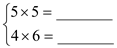 ;
;