Question

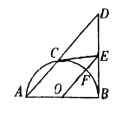
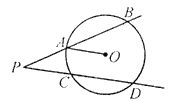
【题目】如图，射线，分别交于点，和点，，且． 已知半径等于5，． 则的长度为__________．

Answer 1

【答案】

【解析】

过O作OM⊥AB于M，ON⊥CD于N，连接OC、OP，求出∠AMO=∠CNO=90°，AM=BM=CN=DN=4，由勾股定理求出OM=ON=3，证Rt△PMO≌Rt△PNO，推出∠MPO=∠NPO，求出∠AOP=∠MPO，推出PA=OA=5，求出PM，根据勾股定理求出即可．

过O作OM⊥AB于M，ON⊥CD于N，连接OC、OP，

则∠AMO=∠CNO=90°，AM=BM=AB=×8=4，CN=DN=4，

∵OA=OC=5，

由勾股定理得：OM=ON=3，

在Rt△PMO和Rt△PNO中

∴Rt△PMO≌Rt△PNO（HL），

∴∠MPO=∠NPO，

∵AO∥PC，

∴∠AOP=∠NPO，

∴∠AOP=∠MPO，

∴PA=OA=5，

∴PM=5+4=9，

在Rt△PMO中，由勾股定理得：，

故答案为：．