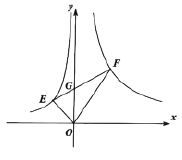
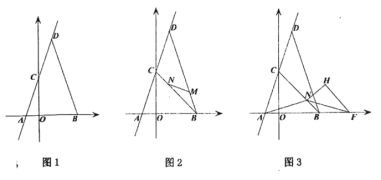
题目内容
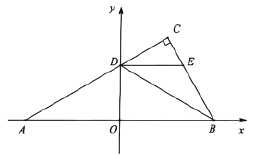
【题目】如图平面直角坐标系中,点![]() ,
,![]() 在
在![]() 轴上,
轴上,![]() ,点
,点![]() 在
在![]() 轴上方,
轴上方,![]() ,
,![]() ,线段
,线段![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() .
.
(1)点![]() 的坐标为 .
的坐标为 .
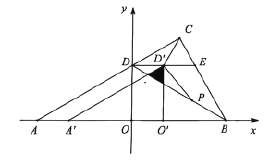
(2)将![]() 沿线段
沿线段![]() 向右平移得
向右平移得![]() ,当点
,当点![]() 与
与![]() 重合时停止运动,记
重合时停止运动,记![]() 与
与![]() 的重叠部分面积为
的重叠部分面积为![]() ,点
,点![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]() 时,求
时,求![]() 的最小值;
的最小值;
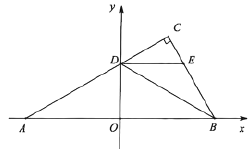
(3)当![]() 移动到点
移动到点![]() 与
与![]() 重合时,将
重合时,将![]() 绕点
绕点![]() 旋转一周,旋转过程中,直线
旋转一周,旋转过程中,直线![]() 分别与直线
分别与直线![]() 、直线
、直线![]() 交于点
交于点![]() 、点
、点![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .当
.当![]() 为直角三角形时,直接写出线段
为直角三角形时,直接写出线段![]() 的长.
的长.
【答案】(1)C(3,3![]() );(2)最小值为2+2
);(2)最小值为2+2![]() ;(3)D0H的值为2
;(3)D0H的值为2![]() -2或2
-2或2![]() +2或4
+2或4![]() -4或4
-4或4![]() +4.
+4.
【解析】
(1)想办法求出A,D,B的坐标,求出直线AC,BC的解析式,构建方程组即可解决问题.
(2)如图2中,设BD交O′D′于G,交A′D′于F.作PH⊥OB于H.利用三角形的面积公式求出点D坐标,再证明PH=![]() PB,把问题转化为垂线段最短即可解决问题.
PB,把问题转化为垂线段最短即可解决问题.
(3)在旋转过程中,符号条件的△GD0H有8种情形,分别画出图形一一求解即可.
(1)如图1中,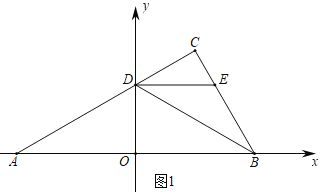
在Rt△AOD中,∵∠AOD=90°,∠OAD=30°,OD=2![]() ,
,
∴OA=![]() OD=6,∠ADO=60°,
OD=6,∠ADO=60°,
∴∠ODC=120°,
∵BD平分∠ODC,
∴∠ODB=![]() ∠ODC=60°,
∠ODC=60°,
∴∠DBO=∠DAO=30°,
∴DA=DB=4![]() ,OA=OB=6,
,OA=OB=6,
∴A(-6,0),D(0,2![]() ),B(6,0),
),B(6,0),
∴直线AC的解析式为y=![]() x+2
x+2![]() ,
,
∵AC⊥BC,
∴直线BC的解析式为y=-![]() x+6
x+6![]() ,
,
由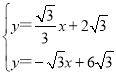 ,解得
,解得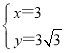 ,
,
∴C(3,3![]() ).
).
(2)如图2中,设BD交O′D′于G,交A′D′于F.作PH⊥OB于H.
∵∠FD′G=∠D′GF=60°,
∴△D′FG是等边三角形,
∵S△D′FG=![]() ,
,
∴D′G=![]() ,
,
∴DD′=![]() GD′=2,
GD′=2,
∴D′(2,2![]() ),
),
∵C(3,3![]() ),
),
∴CD′=![]() =2,
=2,
在Rt△PHB中,∵∠PHB=90°,∠PBH=30°,
∴PH=![]() PB,
PB,
∴CD'+D'P+![]() PB=2+D′P+PH≤2+D′O′=2+2
PB=2+D′P+PH≤2+D′O′=2+2![]() ,
,
∴CD'+D'P+![]() PB的最小值为2+2
PB的最小值为2+2![]() .
.
(3)如图3-1中,当D0H⊥GH时,连接ED0.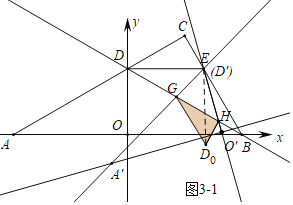
∵ED=ED0,EG=EG.DG=D0G,
∴△EDG≌△ED0G(SSS),
∴∠EDG=∠ED0G=30°,∠DEG=∠D0EG,
∵∠DEB=120°,∠A′EO′=60°,
∴∠DEG+∠BEO′=60°,
∵∠D0EG+∠D0EO′=60°,
∴∠D0EO′=∠BEO′,
∵ED0=EB,E=EH,
∴△EO′D0≌△EO′B(SAS),
∴∠ED0H=∠EBH=30°,HD0=HB,
∴∠CD0H=60°,
∵∠D0HG=90°,
∴∠D0GH=30°,设HD0=BH=x,则DG=GD0=2x,GH=![]() x,
x,
∵DB=4![]() ,
,
∴2x+![]() x+x=4
x+x=4![]() ,
,
∴x=2![]() -2.
-2.
如图3-2中,当∠D0GH=90°时,同法可证∠D0HG=30°,易证四边形DED0H是等腰梯形,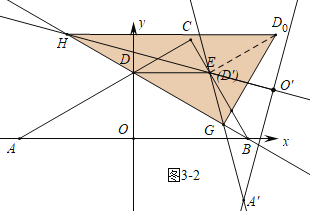
∵DE=ED0=DH=4,可得D0H=4+2×4×cos30°=4+4![]() .
.
如图3-3中,当D0H⊥GH时,同法可证:∠D0GH=30°,
在△EHD0中,由∠D0HE=45°,∠HD0E=30°,ED0=4,可得D0H=4×![]() ,
,
如图3-4中,当DG⊥GH时,同法可得∠D0HG=30°,
设DG=GD0=x,则HD0=BH=2x,GH=![]() x,
x,
∴3x+![]() x=4
x=4![]() ,
,
∴x=2![]() -2,
-2,
∴D0H=2x=4![]() -4.
-4.
如图3-5中,当D0H⊥GH时,同法可得D0H=2![]() -2.
-2.
如图3-6中,当DGG⊥GH时,同法可得D0H=4![]() +4.
+4.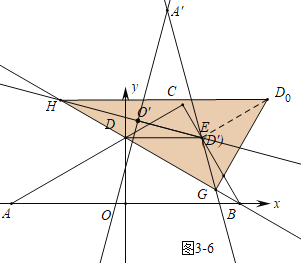
如图3-7中,如图当D0H⊥HG时,同法可得D0H=2![]() +2.
+2.
如图3-8中,当D0G⊥GH时,同法可得HD0=4![]() -4.
-4.
综上所述,满足条件的D0H的值为2![]() -2或2
-2或2![]() +2或4
+2或4![]() -4或4
-4或4![]() +4.
+4.