Question

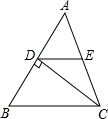
如图，在△ABC中，CD⊥AB于点D，BE⊥AC于点E，F为BC的中点，DE=5，BC=8，则△DEF的周长是(     )

A．21     B．18     C．13     D．15

Answer 1

C【考点】直角三角形斜边上的中线．

【分析】根据直角三角形斜边上的中线等于斜边的一半求出DF、EF，再根据三角形的周长的定义解答．

【解答】解：∵CD⊥AB，F为BC的中点，

∴DF=BC=×8=4，

∵BE⊥AC，F为BC的中点，

∴EF=BC=×8=4，

∴△DEF的周长=DE+EF+DF=5+4+4=13．

故选C．

【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，是基础题，熟记性质并准确识图是解题的关键．