Question

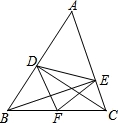
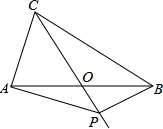
如图，在△ABC中，AB=BC=4，AO=BO，P是射线CO上的一个动点，∠AOC=60°，则当△PAB为直角三角形时，AP的长为__________．

Answer 1

2或2或2．

【考点】勾股定理；含30度角的直角三角形；直角三角形斜边上的中线．

【专题】压轴题；分类讨论．

【分析】利用分类讨论，当∠APB=90°时，易得∠PAB=30°，利用锐角三角函数得AP的长；当∠ABP=90°时，分两种情况讨论，情况一：如图2易得BP，利用勾股定理可得AP的长；情况二：如图3，利用直角三角形斜边的中线等于斜边的一半得出结论．

【解答】解：当∠APB=90°时（如图1），

∵AO=BO，

∴PO=BO，

∵∠AOC=60°，

∴∠BOP=60°，

∴△BOP为等边三角形，

∵AB=BC=4，

∴AP=AB•sin60°=4×=2；

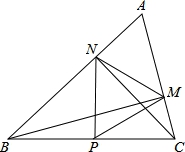
当∠ABP=90°时（如图2），

∵∠AOC=∠BOP=60°，

∴∠BPO=30°，

∴BP===2，

在直角三角形ABP中，

AP==2，

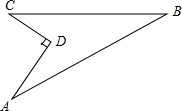
情况二：如图3，∵AO=BO，∠APB=90°，

∴PO=AO，

∵∠AOC=60°，

∴△AOP为等边三角形，

∴AP=AO=2，

故答案为：2或2或2．

【点评】本题主要考查了勾股定理，含30°直角三角形的性质和直角三角形斜边的中线，分类讨论，数形结合是解答此题的关键．