题目内容
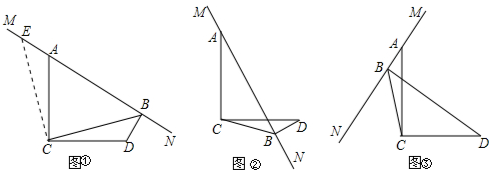
如图,已知∠ACD=90°,MN是过点A的直线,AC=DC,DB⊥MN于B.
(1)当MN绕点B旋转到图①位置时,求证:BD+AB=
CB;
(2)当MN绕点A旋转到图②位置时,BD、AB、CB满足怎样关系式,请直接写答案不必证明;
(3)当MN绕点A旋转到图③位置时,BD、AB、CB之间又存在怎样关系式,请证明你的结论.
(1)当MN绕点B旋转到图①位置时,求证:BD+AB=
| 2 |
(2)当MN绕点A旋转到图②位置时,BD、AB、CB满足怎样关系式,请直接写答案不必证明;
(3)当MN绕点A旋转到图③位置时,BD、AB、CB之间又存在怎样关系式,请证明你的结论.

考点:全等三角形的判定与性质,等腰直角三角形,相似三角形的判定与性质
专题:
分析:(1)过点C作CE⊥CB于点C,与MN交于点E,根据四边形ACDB内角和为360°得到∠EAC=∠BDC,再求出△ECB为等腰直角三角形,进而得到BD+AB=
CB;
(2)过点C作CE⊥CB于点C,与MN交于点E,证明△ACE≌△DCB,则△ECB为等腰直角三角形,据此即可得到BE=
CB,根据BE=AB-AE即可证得;
(3)过点B作BH⊥CD于点H,证明△BDH是等腰直角三角形,求得DH的长,在直角△BCH中,利用直角三角形中30°的锐角所对的直角边等于斜边的一半,即可求得.
| 2 |
(2)过点C作CE⊥CB于点C,与MN交于点E,证明△ACE≌△DCB,则△ECB为等腰直角三角形,据此即可得到BE=
| 2 |
(3)过点B作BH⊥CD于点H,证明△BDH是等腰直角三角形,求得DH的长,在直角△BCH中,利用直角三角形中30°的锐角所对的直角边等于斜边的一半,即可求得.
解答:解:(1)如图①,过点C作CE⊥CB于点C,与MN交于点E
∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°,
∴∠BCD=∠ACE.
∵四边形ACDB内角和为360°,
∴∠BDC+∠CAB=180°.
∵∠EAC+∠CAB=180°,
∴∠EAC=∠BDC.
又∵AC=DC,
在△ACE和△DCB中,
,
∴△ACE≌△DCB(ASA),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=
CB.
又∵BE=AE+AB,
∴BE=BD+AB,
∴BD+AB=
CB.
(2)如图②:AB-BD=
CB.
证明:过点C作CE⊥CB于点C,与MN交于点E,
∵∠ACD=90°,
∴∠ACE=90°-∠DCE,∠BCD=90°-∠ECD,
∴∠BCD=∠ACE.
∵DB⊥MN,
∴∠CAE=90°-∠AFC,∠D=90°-∠BFD,
∵∠AFC=∠BFD,
∴∠CAE=∠D,
又∵AC=DC,
在△ACE和△DCB中,
,
∴△ACE≌△DCB(ASA),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=
CB.
又∵BE=AB-AE,
∴BE=AB-BD,
∴AB-BD=
CB.
如图③BD-AB=
CB.
证明:过点C作CE⊥CB于点C,与MN交于点E,
∵∠ACD=90°,
∴∠ACE=90°+∠ACB,∠BCD=90°+∠ACB,
∴∠BCD=∠ACE.
∵DB⊥MN,
∴∠CAE=90°-∠AFB,∠D=90°-∠CFD,
∵∠AFB=∠CFD,
∴∠CAE=∠D,
又∵AC=DC,
在△ACE和△DCB中,
,
∴△ACE≌△DCB(ASA),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=
CB.
又∵BE=AE-AB,
∴BE=BD-AB,
∴BD-AB=
CB.
(2)MN在绕点A旋转过程中,这个的意思并没有指明是哪种情况,
∴综合了第一个图和第二个图两种情况,
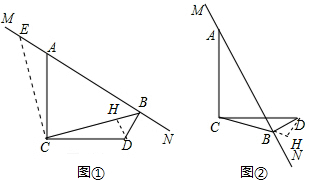 若是第1个图:易证△ACE≌△DCB,CE=CB,
若是第1个图:易证△ACE≌△DCB,CE=CB,
∴△ECB为等腰直角三角形,
∴∠AEC=45°=∠CBD,
过D作DH⊥CB.则△DHB为等腰直角三角形.
BD=
BH,
∴BH=DH=1.
直角△CDH中,∠DCH=30°,
∴CD=2DH=2,CH=
.
∴CB=
+1
若是第二个图:过D作DH⊥CB交CB延长线于H.
解法类似上面,CD=2,但是CB=
-1.
∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°,
∴∠BCD=∠ACE.
∵四边形ACDB内角和为360°,
∴∠BDC+∠CAB=180°.
∵∠EAC+∠CAB=180°,
∴∠EAC=∠BDC.
又∵AC=DC,
在△ACE和△DCB中,
|
∴△ACE≌△DCB(ASA),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=
| 2 |
又∵BE=AE+AB,
∴BE=BD+AB,
∴BD+AB=
| 2 |

(2)如图②:AB-BD=
| 2 |
证明:过点C作CE⊥CB于点C,与MN交于点E,
∵∠ACD=90°,
∴∠ACE=90°-∠DCE,∠BCD=90°-∠ECD,
∴∠BCD=∠ACE.
∵DB⊥MN,
∴∠CAE=90°-∠AFC,∠D=90°-∠BFD,
∵∠AFC=∠BFD,
∴∠CAE=∠D,
又∵AC=DC,
在△ACE和△DCB中,
|
∴△ACE≌△DCB(ASA),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=
| 2 |
又∵BE=AB-AE,
∴BE=AB-BD,
∴AB-BD=
| 2 |
如图③BD-AB=
| 2 |
证明:过点C作CE⊥CB于点C,与MN交于点E,
∵∠ACD=90°,
∴∠ACE=90°+∠ACB,∠BCD=90°+∠ACB,
∴∠BCD=∠ACE.
∵DB⊥MN,
∴∠CAE=90°-∠AFB,∠D=90°-∠CFD,
∵∠AFB=∠CFD,
∴∠CAE=∠D,
又∵AC=DC,
在△ACE和△DCB中,
|
∴△ACE≌△DCB(ASA),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=
| 2 |
又∵BE=AE-AB,
∴BE=BD-AB,
∴BD-AB=
| 2 |
(2)MN在绕点A旋转过程中,这个的意思并没有指明是哪种情况,
∴综合了第一个图和第二个图两种情况,
 若是第1个图:易证△ACE≌△DCB,CE=CB,
若是第1个图:易证△ACE≌△DCB,CE=CB,∴△ECB为等腰直角三角形,
∴∠AEC=45°=∠CBD,
过D作DH⊥CB.则△DHB为等腰直角三角形.
BD=
| 2 |
∴BH=DH=1.
直角△CDH中,∠DCH=30°,
∴CD=2DH=2,CH=
| 3 |
∴CB=
| 3 |
若是第二个图:过D作DH⊥CB交CB延长线于H.
解法类似上面,CD=2,但是CB=
| 3 |
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的性质是全等三角形的对应边相等,对应角相等.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
下列运算结果为正数的是( )
| A、2013-2014 |
| B、(-2014)3 |
| C、(-1)-(-2014) |
| D、-1+(-2014) |
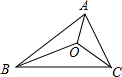 如图所示,BO与CO分别是△ABC的∠ABC和∠ACB的平分线,那么∠BAO与∠CAO的大小关系为( )
如图所示,BO与CO分别是△ABC的∠ABC和∠ACB的平分线,那么∠BAO与∠CAO的大小关系为( )| A、∠BAO>∠CAO |
| B、∠BAO=∠CAO |
| C、∠BAO<∠CAO |
| D、不确定 |
如图所示的QQ表情中,是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
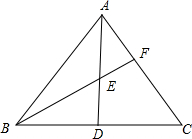 如图,AD是△ABC的中线,E为AD的中点,BE交AC于点F,AF=
如图,AD是△ABC的中线,E为AD的中点,BE交AC于点F,AF= 如图,在Rt△ABC中,∠C=90°,AB=13,BC=5,则以AC为直径的半圆的周长为
如图,在Rt△ABC中,∠C=90°,AB=13,BC=5,则以AC为直径的半圆的周长为