题目内容
2.先化简,再求值:$\frac{{a}^{2}-2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$÷($\frac{1}{b}$-$\frac{1}{a}$),其中a=$\sqrt{5}$+1,b=$\sqrt{5}$-1.分析 先根据分式混合运算的法则把原式进行化简,再把a、b的值代入进行计算即可.
解答 解:原式=$\frac{(a-b)^{2}}{(a+b)(a-b)}$÷$\frac{a-b}{ab}$
=$\frac{a-b}{a+b}$•$\frac{ab}{a-b}$
=$\frac{ab}{a+b}$,
当a=$\sqrt{5}$+1,b=$\sqrt{5}$-1时,原式=$\frac{(\sqrt{5}+1)(\sqrt{5}-1)}{\sqrt{5}+1+\sqrt{5}-1}$=$\frac{4}{2\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
10.如果$\sqrt{x-6}$有意义,那么( )
| A. | x>6 | B. | x≥6 | C. | x<6 | D. | x≤6 |
17.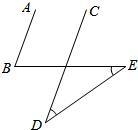 如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )
如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )
 如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )
如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
7.一个不透明的袋中有4个红球,2个白球,除颜色外完全相同,从中随机摸出一个球是白球的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
14.一组数据3、3、5、2、7的中位数和平均数分别是( )
| A. | 3和3 | B. | 3和4 | C. | 4和3 | D. | 4和4 |
12.下列标志中,可以看作是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |