题目内容
 如图,在Rt△ABC中,∠C=90°,AC=12,在△ABE中,DE为AB边上的高,DE=6,S△ABE=60,求BC的长.
如图,在Rt△ABC中,∠C=90°,AC=12,在△ABE中,DE为AB边上的高,DE=6,S△ABE=60,求BC的长.考点:勾股定理
专题:
分析:根据DE=6,S△ABE=60,利用
AB•DE=60,求出AB的长,再根据AC=12利用勾股定理求出BC的长.
| 1 |
| 2 |
解答:解:∵DE=6,S△ABE=60,
∴
AB•DE=60,
∴
AB•6=60,
∴AB=20,
又∵AC=12,
∴BC=
=16.
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴AB=20,
又∵AC=12,
∴BC=
| 202-122 |
点评:本题考查了勾股定理,熟悉三角形的面积和勾股定理的运算是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
若m,n是一个正数的平方根,则( )
| A、m=n | B、m=-n |
| C、m=±n |
方程(m+2)x|m|+4x+3m+1=0是关于x的一元二次方程,则( )
| A、m=±2 | B、m=2 |
| C、m=-2 | D、m≠±2 |
将二次函数y=x2的图象向左平移1个单位,所得图象的函数关系式为( )
| A、y=x2+1 |
| B、y=x2-1 |
| C、y=(x+1)2 |
| D、y=(x-1)2 |
 某农户打算用120米长的围栏围成总面积为800平方米的三个大小相同的矩形羊圈,羊圈的一面靠墙(如图),墙的长度足够,求羊圈的边长AB、BC各多少米?
某农户打算用120米长的围栏围成总面积为800平方米的三个大小相同的矩形羊圈,羊圈的一面靠墙(如图),墙的长度足够,求羊圈的边长AB、BC各多少米?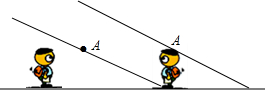 学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.
学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m. 已知AB∥CD,AE平分∠BAC,∠1=55°,求∠C的度数.
已知AB∥CD,AE平分∠BAC,∠1=55°,求∠C的度数. 如图,△ABC中,点D、E分别在AB、AC边上,DE∥BC,∠A=50°,∠C=70°,那么∠ADE的度数是
如图,△ABC中,点D、E分别在AB、AC边上,DE∥BC,∠A=50°,∠C=70°,那么∠ADE的度数是