题目内容
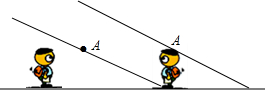 学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.
学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,求其影子B1C1的长.
考点:相似三角形的应用,中心投影
专题:
分析:(1)根据题意画出图形即可;
(2)根据题意得到△ABC∽△GHC,根据相似三角形的性质得到
=
,代入即可求出答案;
(3)与(2)类似得到△A1B1C1∽△GHC1,根据相似三角形的性质推出
=
,代入即可求出答案.
(2)根据题意得到△ABC∽△GHC,根据相似三角形的性质得到
| AB |
| GH |
| BC |
| HC |
(3)与(2)类似得到△A1B1C1∽△GHC1,根据相似三角形的性质推出
| A1B1 |
| GH |
| B1C1 |
| HC1 |
解答: 解:(1)如图:形成影子的光线,路灯灯泡所在的位置G.
解:(1)如图:形成影子的光线,路灯灯泡所在的位置G.
(2)由题意得:△ABC∽△GHC,
∴
=
,
∴
=
,
解得:GH=4.8(m),
答:路灯灯泡的垂直高度GH是4.8m.
(3)∵△A1B1C1∽△GHC1,
∴
=
,
设B1C1长为xm,
则
=
,
解得:x=1.5(m),
即B1C1=1.5(m).
答:小明的影子B1C1的长是1.5m.
 解:(1)如图:形成影子的光线,路灯灯泡所在的位置G.
解:(1)如图:形成影子的光线,路灯灯泡所在的位置G.(2)由题意得:△ABC∽△GHC,
∴
| AB |
| GH |
| BC |
| HC |
∴
| 1.6 |
| GH |
| 3 |
| 6+3 |
解得:GH=4.8(m),
答:路灯灯泡的垂直高度GH是4.8m.
(3)∵△A1B1C1∽△GHC1,
∴
| A1B1 |
| GH |
| B1C1 |
| HC1 |
设B1C1长为xm,
则
| 1.6 |
| 4.8 |
| x |
| x+3 |
解得:x=1.5(m),
即B1C1=1.5(m).
答:小明的影子B1C1的长是1.5m.
点评:本题主要考查对相似三角形的性质,相似三角形的应用,解一元一次方程等知识点的理解和掌握,把实际问题转化成数学问题是解此题的关键,题型较好,用的数学思想是转化思想.

练习册系列答案
相关题目
下列图形中,绕某个点旋转180°后能与自身重合的有( )
①矩形;②等边三角形;③线段;④平行四边形.
①矩形;②等边三角形;③线段;④平行四边形.
| A、4个 | B、3个 | C、2个 | D、1个 |
以下计算正确的是( )
| A、a2•a3=a6 |
| B、(a-b)2=a2-b2 |
| C、(a2b)2=a4b |
| D、(4a2+a)÷a=4a+1 |
下列说法错误的是( )
| A、任何有理数都有倒数 |
| B、互为倒数的两个数的积为1 |
| C、互为倒数的两个数同号 |
| D、-1的倒数是-1 |
 完成下面的说理过程,并在括号内填写理由.
完成下面的说理过程,并在括号内填写理由. (1)已知PA切⊙O于点A,PB切⊙O于点B,PO=4,PA=2
(1)已知PA切⊙O于点A,PB切⊙O于点B,PO=4,PA=2
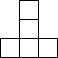
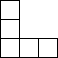
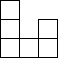
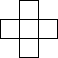 用8个相同的小正方形搭成一个几何体,其俯视图如图所示,那么这个几何体的左视图一定不是( )
用8个相同的小正方形搭成一个几何体,其俯视图如图所示,那么这个几何体的左视图一定不是( )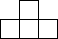
 如图,在Rt△ABC中,∠C=90°,AC=12,在△ABE中,DE为AB边上的高,DE=6,S△ABE=60,求BC的长.
如图,在Rt△ABC中,∠C=90°,AC=12,在△ABE中,DE为AB边上的高,DE=6,S△ABE=60,求BC的长.