题目内容
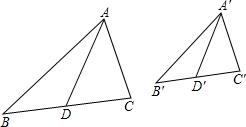如图，△ABC∽△A′B′C′，AD、A′D′分别是它们的中线，求证：AD：A′D′=AB：A′B′．考点：相似三角形的性质
专题：证明题
分析：利用相似三角形的性质得出
=
，进而求出△ABD∽△A′B′D′，即可得出答案．
| AB |
| A′B′ |
| BD |
| B′D′ |
解答：证明：∵△ABC∽△A′B′C′，
∴∠B=∠B′，AD、A′D′分别是它们的中线，
∴
=
，
∴△ABD∽△A′B′D′，
∴AD：A′D′=AB：A′B′．
∴∠B=∠B′，AD、A′D′分别是它们的中线，
∴
| AB |
| A′B′ |
| BD |
| B′D′ |
∴△ABD∽△A′B′D′，
∴AD：A′D′=AB：A′B′．
点评：此题主要考查了相似三角形的判定与性质，得出△ABD∽△A′B′D′是解题关键．
练习册系列答案
相关题目
如图是一个正六棱柱的建筑物，画出它的三视图．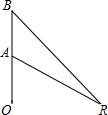
如图，一枚运载火箭从地面O处发射，当火箭到达点A处时，地面R处的雷达站测得AR的距离是6km，仰角为30°．5s后，火箭到达点B处，此时BR的距离为6.25km，仰角为45°．求火箭从A处到B处的平均速度（结果精确到1m/s）
如图所示：∠AOB的内部有一点P，到顶点O的距离为5cm，M、N分别是射线OA、OB上的动点．若∠AOB=30°，则△PMN周长的最小值为