题目内容
17.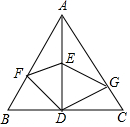 如图,在边长为8的等边三角形ABC中,点E是中线AD的中点,点F在AB边上,点G在AC边上,则由线段DG、GE、EF、FD围成的图形周长最小值等于12.
如图,在边长为8的等边三角形ABC中,点E是中线AD的中点,点F在AB边上,点G在AC边上,则由线段DG、GE、EF、FD围成的图形周长最小值等于12.
分析 如图,作点D关于直线AB、直线AC的对称点M、N,连接EM、EN交AB、AC于点F、点G,连接EK.此时由线段DG、GE、EF、FD围成的图形周长最小,只要证明MN∥BC,FG是△ABC的中位线即可解决问题.
解答 解:如图,作点D关于直线AB、直线AC的对称点M、N,连接EM、EN交AB、AC于点F、点G,连接EK.
∵FE+FD=FM+EF=EM,
根据两点之间线段最短,可知此时FE+FD最短,同理GE+GD最短.即此时DG、GE、EF、FD围成的图形周长最小
∵△ABC是等边三角形,点E是中线AD的中点,
∴AD⊥BD,∠B=60°,∠BDK=∠BAD=30°,∠ADK=60°,
∴AD=2DK,
∴DE=DK,
∴△EDK是等边三角形,
∴∠EKD=∠KED=60°,
∵KM=KD=DE=EK,
∴∠M=∠KEM=30°,
∴∠MED=90°,同理∠NED=90°,
∴M、E、N共线,MN∥BC,
∵AE=ED,
∴AF=FB,AG=GC,
∴FG=$\frac{1}{2}$BC=4,DF=DG=$\frac{1}{2}$AB=4,
∴DG、GE、EF、FD围成的图形周长最小值为12.
故答案为12.
点评 本题考查等边三角形的性质、轴对称-最短问题、平行线等分线段定理、三角形中位线定理等知识,解题的关键是学会利用对称,探究最小值问题,属于中考常考题型.

练习册系列答案
相关题目
7.下列说法正确的是( )
| A. | 有理数分为正数和负数 | B. | 有理数都有相反数 | ||
| C. | 倒数等于它本身的数只有一个 | D. | 若a为有理数,则-a一定是负数 |
9.在实数$\sqrt{2}$,π,$\frac{3}{7}$,-$\root{3}{8}$,2.1616…,2.1010010001…(每两个1之间依次多1个0)中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
5.据不完全统计,2016年国庆期间来北京旅游的人数达700000人,用科学记数法可表示700000为( )
| A. | 0.7×105 | B. | 0.7×106 | C. | 7×105 | D. | 7×106 |
 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于点E,AB=5,AC=3,则△ACE的周长为7.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于点E,AB=5,AC=3,则△ACE的周长为7.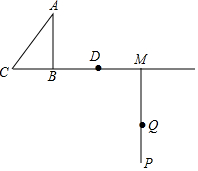 如图,Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D从B点出发,沿射线CB方向以每秒3个单位长度的速度运动,射线MP⊥射线CB,且BM=10,点Q从M点出发,沿射线MQ方向以每秒a个单位长度的速度运动,己知D,Q两点同时出发,记时间为t.
如图,Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D从B点出发,沿射线CB方向以每秒3个单位长度的速度运动,射线MP⊥射线CB,且BM=10,点Q从M点出发,沿射线MQ方向以每秒a个单位长度的速度运动,己知D,Q两点同时出发,记时间为t.