题目内容
9. 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于点E,AB=5,AC=3,则△ACE的周长为7.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于点E,AB=5,AC=3,则△ACE的周长为7.
分析 先根据勾股定理求出BC的长,再由线段垂直平分线的性质即可得出结论.
解答 解:∵在Rt△ABC中,∠C=90°,AB=5,AC=3,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4.
∵AB的垂直平分线交BC于点E,
∴AE=BE,
∴△ACE的周长=AC+BC=3+4=7.
故答案为:7.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
2.下列方程中,关于x的一元二次方程是( )
| A. | x2-2x-3=0 | B. | x2-2y-1=0 | C. | x2-x(x+3)=0 | D. | ax2+bx+c=0 |
2.某学校准备食建一个面积为200m2的矩形花圃,它的长比宽多10m,设花圃的宽为x m.则可列方程为( )
| A. | x (x-10)=200 | B. | 2x+2 (x-10)=200 | C. | x(x+10)=200 | D. | 2x+2(x+10)=200 |
17.下列各组算式中,结果为负数的是( )
| A. | -(-5) | B. | -|-5| | C. | (-3)×(-5) | D. | (-5)2 |
4. 如图,OP是∠AOB的平分线,点C、D分别在∠AOB的两边OA、OB上,添加下列条件,不能判定△POC≌△POD的选项是( )
如图,OP是∠AOB的平分线,点C、D分别在∠AOB的两边OA、OB上,添加下列条件,不能判定△POC≌△POD的选项是( )
 如图,OP是∠AOB的平分线,点C、D分别在∠AOB的两边OA、OB上,添加下列条件,不能判定△POC≌△POD的选项是( )
如图,OP是∠AOB的平分线,点C、D分别在∠AOB的两边OA、OB上,添加下列条件,不能判定△POC≌△POD的选项是( )| A. | ∠OPC=∠OPD | B. | PC=PD | C. | PC⊥OA,PD⊥OB | D. | OC=OD |
18. 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )
 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6cm,则△DEB的周长为( )| A. | 40cm | B. | 6cm | C. | 8cm | D. | 10cm |
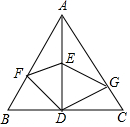 如图,在边长为8的等边三角形ABC中,点E是中线AD的中点,点F在AB边上,点G在AC边上,则由线段DG、GE、EF、FD围成的图形周长最小值等于12.
如图,在边长为8的等边三角形ABC中,点E是中线AD的中点,点F在AB边上,点G在AC边上,则由线段DG、GE、EF、FD围成的图形周长最小值等于12.