题目内容
7.解不等式组并把解表示在数轴上:$\left\{\begin{array}{l}2(x+3)≤3-5(x-2)\\ \frac{x+1}{3}-\frac{2x-1}{2}<1\end{array}\right.$.分析 根据不等式的性质分别求出每个不等式的解集,根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{2(x+3)≤3-5(x-2)①}\\{\frac{x+1}{3}-\frac{2x-1}{2}<1②}\end{array}\right.$,
解①得x≤1,
解②得x>-$\frac{1}{4}$,
所以不等式组的解集为-$\frac{1}{4}$<x≤1,
用数轴表示为: .
.
点评 本题考查了解一元一次不等式组:分别求出不等式组各不等式的解集,然后根据“同大取大,同小取小,大于小的小于大的取中间,大于大的小于小的无解”确定不等式组的解集.也考查了在数轴上表示不等式的解集.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列说法,正确的是( )
| A. | 每个命题都有逆命题 | B. | 假命题的逆命题一定是假命题 | ||
| C. | 每个定理都有逆定理 | D. | 真命题是逆命题一定是真命题 |
2.小李在杭州某水果市场批发30筐苹果,以每筐25千克为标准,超过或不足的分别用正、负来表示,记录如下:
(1)30筐苹果中,最重的一筐比最轻的一筐要重多少千克?
(2)与标准质量比较,30筐苹果总计超过或不足多少千克?
(3)若苹果每千克批发价是7元,小李以每千克10元的价格销售,在销售600千克苹果后,剩余苹果的售价定为每千克8元,这次销售中的运输成本和其他费用为240元.求小李出售这30筐苹果共获利多少元?
| 与标准质量的差(单位:千克) | -2 | -1 | -1.5 | 0 | 1 | 1.5 |
| 筐数 | 2 | 5 | 3 | 10 | 4 | 6 |
(2)与标准质量比较,30筐苹果总计超过或不足多少千克?
(3)若苹果每千克批发价是7元,小李以每千克10元的价格销售,在销售600千克苹果后,剩余苹果的售价定为每千克8元,这次销售中的运输成本和其他费用为240元.求小李出售这30筐苹果共获利多少元?
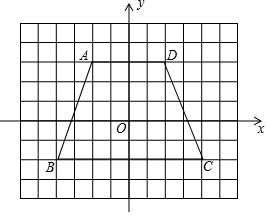 (1)写出如图所示的四边形ABCD各顶点的坐标.
(1)写出如图所示的四边形ABCD各顶点的坐标. 如图,在矩形ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,有列结论:①AF=AE ②EF=2$\sqrt{5}$③AF=EF④S△AEF=10,其中正确的结论有①②④.(填序号)
如图,在矩形ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,有列结论:①AF=AE ②EF=2$\sqrt{5}$③AF=EF④S△AEF=10,其中正确的结论有①②④.(填序号)